Bài 2.24 trang 27 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.24 trang 27 Sách bài tập Toán 10 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Một hợp tác xã chăn nuôi dự định trộn hai loại thức ăn gia súc X và gia súc Y để tạo thành thức ăn hỗn hợp cho gia súc.
Đề bài
Một hợp tác xã chăn nuôi dự định trộn hai loại thức ăn gia súc \(X\) và gia súc \(Y\) để tạo thành thức ăn hỗn hợp cho gia súc. Giá một bao loại \(X\) là 250 nghìn đồng, giá một bao loại \(Y\) là 200 nghìn đồng. Mỗi bao loại \(X\) chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C. Mỗi bao loại \(Y\) chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C. Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc \(X\) và \(Y\) sao cho hỗn hợp thu được tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C.
A. \(1,95\) triệu đồng.
B. \(4,5\) triệu đồng.
C. \(1,85\) triệu đồng.
D. \(1,7\) triệu đồng.
Phương pháp giải - Xem chi tiết
- Viết hệ bất phương trình từ bài toán trên
- Xác định miền nghiệm của hệ bất phương trình đó
- Viết biểu thức biểu thị chi phí để mua hai loại thức ăn gia súc loại \(X\) và \(Y\)
- Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc loại \(X\) và \(Y\) từ miền nghiệm vừa tìm được.
Lời giải chi tiết
Số lượng chất dinh dưỡng A cần dùng để tạo thành hai loại thức ăn gia súc \(X\) và \(Y\) là: \(2x + y \ge 12.\)
Số lượng chất dinh dưỡng B cần dùng để tạo thành hai loại thức ăn gia súc \(X\) và \(Y\) là: \(2x + 9y \ge 36.\)
Số lượng chất dinh dưỡng C cần dùng để tạo thành hai loại thức ăn gia súc \(X\) và \(Y\) là: \(2x + 3y \ge 24.\)
Từ đó, ta có hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{2x + y \ge 12.}\\{2x + 9y \ge 36.}\\{2x + 3y \ge 24.}\end{array}} \right.\)
Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bờ \(d:x = 0\) chứa điểm \(\left( {1;0} \right).\)
Miền nghiệm của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \({d_1}:y = 0\) chứa điểm \(\left( {0;1} \right).\)
Miền nghiệm của bất phương trình \(2x + y \ge 12\) là nửa mặt phẳng bờ \({d_2}:2x + y = 12\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(2x + 9y \ge 36\) là nửa mặt phẳng bờ \({d_3}:2x + 9y = 36\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(2x + 3y \ge 24\) là nửa mặt phẳng bờ \({d_4}:2x + 3y = 24\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)
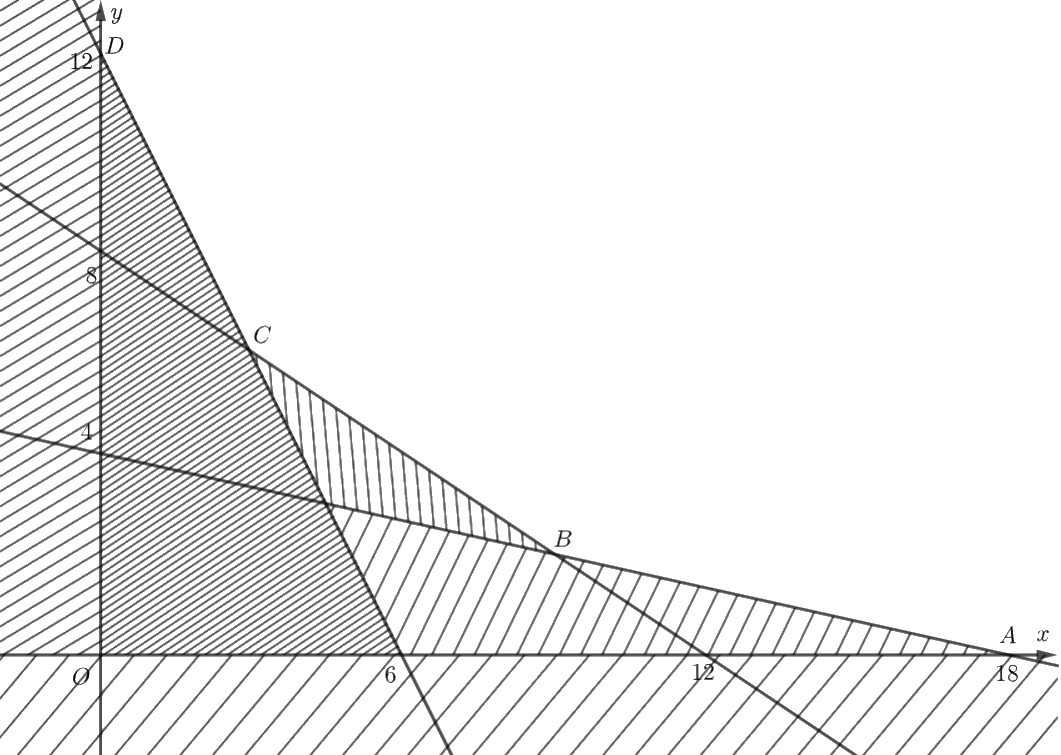
Miền nghiệm của hệ bất phương trình là: miền không bị gạch với các đỉnh \(A\left( {18;0} \right),\) \(B\left( {9;2} \right),\) \(C\left( {3;6} \right),\) \(D\left( {0;12} \right).\)
\(F\left( {3;6} \right) = 250.3 + 200.6 = 1950,\,\,F\left( {0;12} \right) = 250.0 + 200.12 = 2400.\)
Vậy chi phí nhỏ nhất để mua hai loại thức ăn gia súc loại \(X\) và \(Y\) là: \(F\left( {3;6} \right) = 1950.\)
Chọn A.
Bài 2.24 trang 27 Sách bài tập Toán 10 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài 2.24 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 2.24, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu:
Cho hình vuông ABCD có cạnh bằng a. Gọi M là trung điểm của cạnh BC. Tính độ dài của vectơ AM.
Lời giải:
Vậy độ dài của vectơ AM là (a√5)/2.
Để giải các bài tập về vectơ một cách hiệu quả, các em học sinh nên:
Vectơ không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau, như:
Để củng cố kiến thức về vectơ, các em học sinh có thể tự giải các bài tập sau:
Bài 2.24 trang 27 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.