Chào mừng các em học sinh đến với lời giải chi tiết bài 1.9 trang 11 sách bài tập Toán 10 - Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Điền Đ vào ô trống nếu mệnh đề đúng, điền S vào ô trống nếu mệnh đề sai.
Đề bài
Điền Đ vào ô trống nếu mệnh đề đúng, điền S vào ô trống nếu mệnh đề sai.
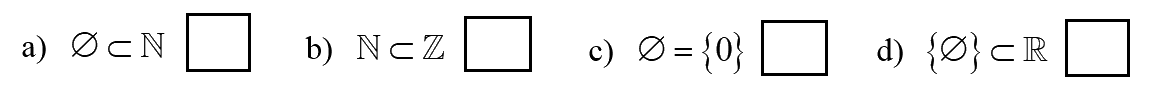
Phương pháp giải - Xem chi tiết
+Tập hợp rỗng: \(\emptyset\), là tập không có phần tử nào.
+ \(A \subset B \Leftrightarrow \forall x \in A:x \in B\)
đặc biệt: \(\emptyset \subset A,\forall A.\)
Lời giải chi tiết
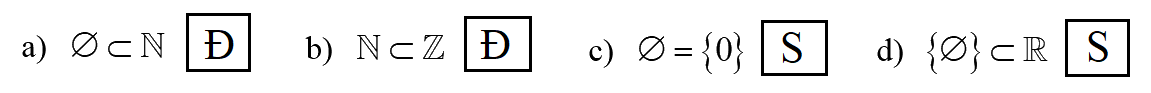
c) Sai vì \(\emptyset\) là tập không có phần tử nào, còn \(\{0\}\) là tập có một phần tử là 0.
d) Sai vì kì hiệu \(\emptyset\) là tập hợp, không phải phần tử nên viết \(\{\emptyset\}\) là sai.
Bài 1.9 trang 11 sách bài tập Toán 10 - Kết nối tri thức thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu, phần bù) để giải quyết các bài toán cụ thể. Việc hiểu rõ các khái niệm và tính chất của tập hợp là nền tảng quan trọng để giải quyết bài tập này một cách hiệu quả.
Bài 1.9 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh xác định các tập hợp, thực hiện các phép toán trên tập hợp và chứng minh các đẳng thức liên quan đến tập hợp. Các bài tập được thiết kế để giúp học sinh rèn luyện kỹ năng phân tích, suy luận logic và áp dụng kiến thức vào thực tế.
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng câu hỏi cụ thể:
Cho A = {1; 2; 3; 4} và B = {3; 4; 5; 6}. Tìm A ∪ B và A ∩ B.
Cho C = {a; b; c; d} và D = {b; d; e; f}. Tìm C \ D và D \ C.
Cho E = {1; 2; 3} và F = {2; 4; 6}. Tìm E ∪ F và E ∩ F.
Giả sử ta có hai tập hợp: X = {1, 3, 5, 7} và Y = {2, 3, 6, 7}.
| Phép toán | Kết quả |
|---|---|
| X ∪ Y | {1, 2, 3, 5, 6, 7} |
| X ∩ Y | {3, 7} |
| X \ Y | {1, 5} |
| Y \ X | {2, 6} |
Bài 1.9 trang 11 sách bài tập Toán 10 - Kết nối tri thức là một bài tập cơ bản nhưng quan trọng để giúp học sinh nắm vững kiến thức về tập hợp. Hy vọng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin hơn trong quá trình học tập và giải quyết các bài tập tương tự.