Bài 2.17 trang 25 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.17 trang 25 Sách bài tập Toán 10 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Miền nghiệm của hệ bất phương trình nào dưới đây là miền tam giác ABC (miền không bị gạch) ?
Đề bài
Miền nghiệm của hệ bất phương trình nào dưới đây là miền tam giác \(ABC\) (miền không bị gạch)?
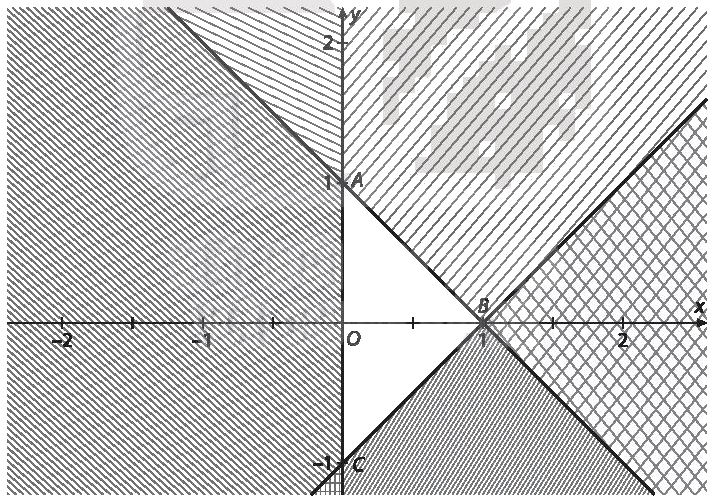
A. \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \ge 1}\\{x \ge 0}\end{array}.} \right.\)
B. \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \le 1}\\{x \ge 0}\end{array}} \right..\)
C. \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge - 1}\\{x + y \ge - 1}\\{x \ge 0}\end{array}.} \right.\)
D. \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge - 1}\\{x + y \ge - 1}\\{y \ge 0}\end{array}.} \right.\)
Lời giải chi tiết
Dễ thấy đáp án D sai.
Thay điểm \(O\left( {0;0} \right)\) vào bất phương trình, \(x - y \ge 1\)ta được:
\(0 - 0 = 0 > 1\) (vô lý)
\( \Rightarrow \) loại đáp án A.
Thay điểm \(O\left( {0;0} \right)\) vào bất phương trình, \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \le 1}\\{x \ge 0}\end{array}} \right.\) ta được:
\(\left\{ {\begin{array}{*{20}{c}}{0 + 0 = 0 < 1}\\{0 - 0 < 1}\\{0 \ge 0}\end{array}} \right.\) (thỏa mãn)
\( \Rightarrow \) đáp án B đúng.
Chọn B.
Bài 2.17 trang 25 Sách bài tập Toán 10 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài 2.17 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 2.17 trang 25, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu:
Cho hình vuông ABCD có cạnh bằng a. Gọi M là trung điểm của cạnh BC. Tính độ dài của vectơ AM.
Lời giải:
Vậy độ dài của vectơ AM là (a√5)/2.
Để giải các bài tập về vectơ một cách hiệu quả, các em học sinh nên:
Ngoài sách giáo khoa và sách bài tập, các em học sinh có thể tham khảo thêm các tài liệu sau:
Bài 2.17 trang 25 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc học tập môn Toán.