Bài 4.56 trang 69 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập này một cách hiệu quả.
Cho tam giác ABC đều các cạnh có độ dài bằng 1
Đề bài
Cho tam giác \(ABC\) đều các cạnh có độ dài bằng 1. Lấy \(M,\,\,N,\,\,P\) tương ứng thuộc các cạnh \(BC,\,\,CA,\,\,AB\) sao cho \(BM = 2MC,\,\,CN = 2NA\) và \(AM \bot NP.\) Tỉ số của \(\frac{{AP}}{{AB}}\) bằng
A. \(\frac{5}{{12}}\)
B. \(\frac{7}{{12}}\)
C. \(\frac{5}{7}\)
D. \(\frac{7}{5}\)
Phương pháp giải - Xem chi tiết
- Đặt \(AP = x\) \(\left( {0 < x < 1} \right)\)
- Biểu diễn các vectơ \(\overrightarrow {PN} \) và \(\overrightarrow {AM} \) theo các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)
- Tìm x dựa vào tích vô hướng của hai vectơ \(\overrightarrow {AM} .\overrightarrow {PN} = 0\)
Lời giải chi tiết
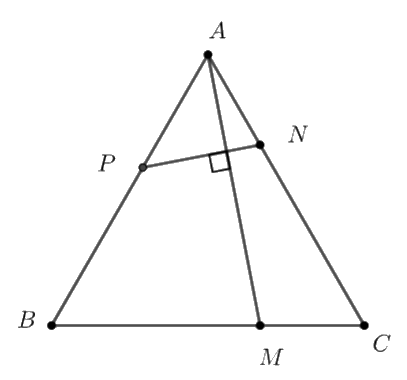
Đặt \(AP = x\) \(\left( {0 < x < 1} \right)\)
Ta có: \(\overrightarrow {PN} = \overrightarrow {PA} + \overrightarrow {AN} = \frac{1}{3}\overrightarrow {AC} - x\overrightarrow {AB} \)
Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {BC} = \overrightarrow {AB} + \frac{2}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \)
Ta có: \(AM \bot PN\) \( \Rightarrow \) \(\overrightarrow {AM} .\overrightarrow {PN} = 0\)
\( \Leftrightarrow \) \(\left( {\frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} } \right).\left( {\frac{1}{3}\overrightarrow {AC} - x\overrightarrow {AB} } \right) = 0\)
\( \Leftrightarrow \) \(\frac{1}{9}\overrightarrow {AB} .\overrightarrow {AC} - \frac{x}{3}{\overrightarrow {AB} ^2} + \frac{2}{9}{\overrightarrow {AC} ^2} - \frac{{2x}}{3}\overrightarrow {AC} .\overrightarrow {AB} = 0\)
\( \Leftrightarrow \) \(\frac{1}{9}.\frac{1}{2} - \frac{x}{3} + \frac{2}{9} - \frac{{2x}}{3}.\frac{1}{2} = 0\)
\( \Leftrightarrow \) \(\frac{1}{{18}} - \frac{x}{3} + \frac{2}{9} - \frac{x}{3} = 0\)
\( \Leftrightarrow \) \(1 - 6x + 4 - 6x = 0\)
\( \Leftrightarrow \) \(12x = 5\) \( \Leftrightarrow \) \(x = \frac{5}{{12}}\)
Vậy \(\frac{{AP}}{{AB}} = \frac{5}{{12}}\)
Chọn A.
Bài 4.56 trang 69 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ về vectơ, các phép toán vectơ và cách áp dụng chúng vào giải quyết vấn đề.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Đề bài thường cung cấp thông tin về các vectơ, vị trí của các điểm và yêu cầu tính toán một đại lượng nào đó liên quan đến vectơ.
Để giải bài 4.56 trang 69, chúng ta sẽ thực hiện theo các bước sau:
Ví dụ, nếu đề bài yêu cầu tính độ dài của một đoạn thẳng, chúng ta có thể sử dụng công thức tính độ dài của vectơ để giải quyết. Nếu đề bài yêu cầu chứng minh ba điểm thẳng hàng, chúng ta có thể sử dụng điều kiện ba điểm thẳng hàng dựa trên vectơ.
Ngoài bài 4.56, còn rất nhiều bài tập tương tự trong sách bài tập Toán 10 - Kết nối tri thức với cuộc sống. Các bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán về hình học phẳng, hình học không gian và các bài toán ứng dụng thực tế.
Vectơ có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 4.56 trang 69 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải bài tập. Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ giải bài tập này một cách dễ dàng và hiệu quả.
Hãy truy cập giaitoan.edu.vn để tìm thêm nhiều bài giải toán 10 và các tài liệu học tập hữu ích khác.