Bài 4.5 trang 47 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.5 trang 47, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC không vuông, với trực tâm H, nội tiếp đường tròn (O). Kẻ đường kính AA' của đường tròn (O).
Đề bài
Cho tam giác \(ABC\) không vuông, với trực tâm \(H\), nội tiếp đường tròn \((O).\) Kẻ đường kính \(AA'\) của đường tròn \((O).\)
a) Chứng minh rằng \(\overrightarrow {BH} = \overrightarrow {A'C} .\)
b) Gọi \(M\) là trung điểm của \(BC.\) Tìm mối quan hệ về phương, hướng và độ dài của hai vectơ \(\overrightarrow {AH} \) và \(\overrightarrow {OM} .\)
Phương pháp giải - Xem chi tiết
- Chứng minh tứ giác \(ABHC\) là hình bình hành
- Chứng minh \(M\) là trung điểm của \(A'H\)
- Chứng minh \(MO\) là đường trung bình của \(\Delta AA'H\)
Lời giải chi tiết
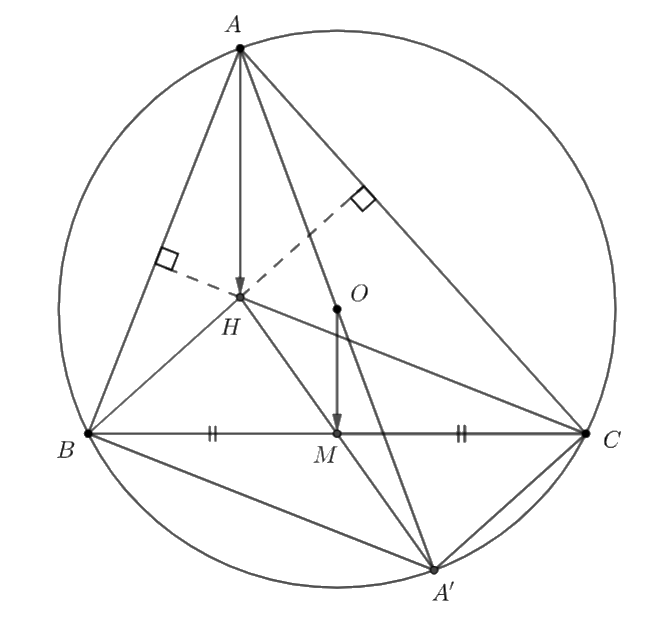
a) Xét \((O)\) có: \(\widehat {ABA'} = \widehat {ACA'} = {90^ \circ }\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow A'C \bot AC\) và \(A'B \bot AB\) (1)
Ta có: \(H\) là trực tâm của tam giác \(ABC.\)
\( \Rightarrow BH \bot AC\) và \(CH \bot AB\) (2)
Từ (1) và (2) \( \Rightarrow \) \(BH\)//\(A'C\) và \(A'B\)//\(CH.\)
Xét tứ giác \(ABHC\) có: \(BH\)//\(A'C\) và \(A'B\)//\(CH\)
\( \Rightarrow \) tứ giác \(ABHC\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \overrightarrow {BH} = \overrightarrow {A'C} \)
b) Ta có: tứ giác \(ABHC\) là hình bình hành
nên \(M\) là trung điểm của \(A'H\)
Xét \(\Delta AA'H\) có: \(M\) là trung điểm của \(A'H\)
\(O\) là trung điểm của \(AA'\)
\( \Rightarrow \) \(MO\) là đường trung bình của \(\Delta AA'H\)
\( \Rightarrow \) \(MO\)//\(AH\) và \(2MO = AH\)
\( \Rightarrow \) hai vectơ \(\overrightarrow {MO} ,\,\,\overrightarrow {AH} \) cùng hướng và \(2\overrightarrow {OM} = \overrightarrow {AH} .\)
Bài 4.5 trang 47 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống thuộc chương trình học Toán 10, tập trung vào việc củng cố kiến thức về vectơ và ứng dụng của chúng. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Dưới đây là lời giải chi tiết bài 4.5 trang 47 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống:
Đề bài yêu cầu (giả sử đề bài là: Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo vectơ AB và AC).
Để tìm vectơ AM, ta có thể sử dụng quy tắc trung điểm của đoạn thẳng. Theo quy tắc này, vectơ AM bằng một nửa tổng của vectơ AB và vectơ AC.
Ta có: M là trung điểm của BC nên BM = MC. Do đó:
AM = (AB + AC) / 2
Vậy, vectơ AM được biểu diễn theo vectơ AB và AC là: AM = (AB + AC) / 2
Lời giải trên dựa trên quy tắc trung điểm của đoạn thẳng, một công cụ quan trọng trong việc làm việc với vectơ. Việc hiểu rõ quy tắc này giúp học sinh giải quyết các bài toán liên quan đến trung điểm, trọng tâm và các điểm đặc biệt khác trong hình học một cách dễ dàng.
Để củng cố kiến thức về vectơ và ứng dụng của chúng, học sinh có thể làm thêm các bài tập tương tự sau:
Ngoài các ứng dụng trong hình học, vectơ còn được sử dụng rộng rãi trong vật lý để biểu diễn các đại lượng vật lý như lực, vận tốc, gia tốc. Việc hiểu rõ về vectơ giúp học sinh có cái nhìn sâu sắc hơn về thế giới xung quanh.
Để học tốt môn Toán 10, đặc biệt là phần vectơ, học sinh cần:
Hy vọng với lời giải chi tiết và những phân tích trên, các em học sinh sẽ hiểu rõ hơn về bài 4.5 trang 47 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống và tự tin hơn trong quá trình học tập.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Quy tắc trung điểm | Vectơ nối trung điểm của một cạnh với đỉnh đối diện bằng một nửa tổng của hai vectơ tạo thành cạnh đó. |