Bài 6.34 trang 22 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.34 trang 22, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Các đường dưới đây, đường nào không là đồ thị hàm số?
Đề bài
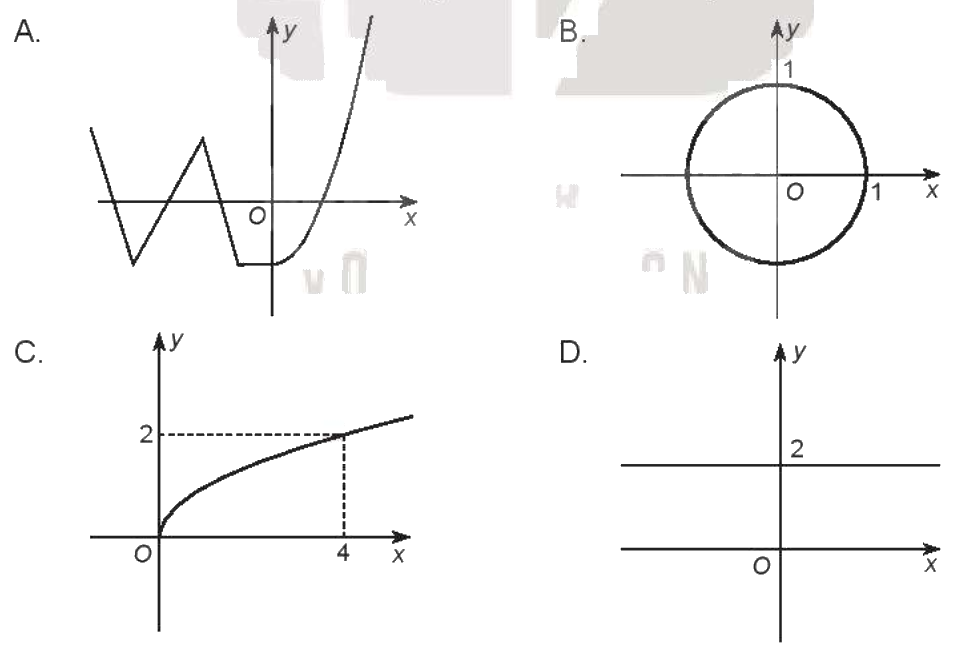
Các đường dưới đây, đường nào không là đồ thị hàm số?
Lời giải chi tiết
Xét đồ thị B ta thấy điểm (0 ; 1) và (0 ; -1) thuộc ĐTHS. Như vậy với x = 0 ta có y = 1 hoặc y = -1, điều này vi phạm định nghĩa về hàm số (với mỗi giá trị x thuộc tập xác định chỉ cho duy nhất một giá trị y tương ứng)
\( \Rightarrow \) Chọn B
Bài 6.34 trang 22 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vectơ trong hình học. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Đề bài: (Giả sử đề bài cụ thể của bài 6.34 được đưa ra ở đây. Ví dụ: Cho tam giác ABC, tìm tọa độ điểm D sao cho...)
Lời giải:
Ví dụ minh họa: (Giả sử đề bài là: Cho tam giác ABC với A(1;2), B(3;4), C(5;0). Tìm tọa độ điểm D sao cho ABDC là hình bình hành.)
Giải:
Để ABDC là hình bình hành, ta cần có AB = DC. Gọi D(x;y). Khi đó:
AB = (3-1; 4-2) = (2; 2)
DC = (5-x; 0-y) = (5-x; -y)
Để AB = DC, ta có hệ phương trình:
2 = 5 - x
2 = -y
Giải hệ phương trình, ta được x = 3 và y = -2. Vậy D(3; -2).
Lưu ý:
Các bài tập tương tự:
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 6.34 trang 22 sách bài tập Toán 10 Kết nối tri thức. Chúc các em học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tích vô hướng | Một phép toán giữa hai vectơ cho ra một số. |