Bài 5.13 trang 80 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.13 trang 80, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hai biểu đồ chấm điểm biểu diễn hai mẫu số liệu A, B như sau:
Đề bài
Cho hai biểu đồ chấm điểm biểu diễn hai mẫu số liệu A, B như sau:
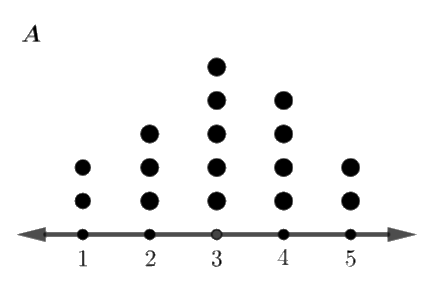
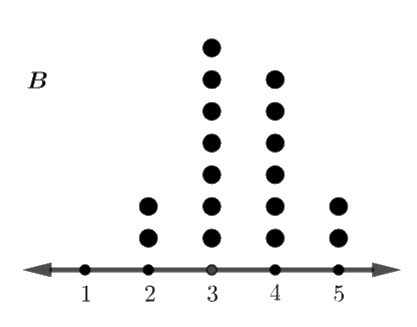
Trong đó, mỗi chấm biểu diễn một giá trị trong mẫu số liệu.
Không tính, hãy cho biết:
a) Độ lệch chuẩn của mẫu số liệu nào lớn hơn.
b) Khoảng biến thiên của hai mẫu số liệu có như nhau không.
Phương pháp giải - Xem chi tiết
- Quan sát biểu đồ và nhận xét sự phân tán của các giá trị, mẫu có số liệu đồng đều thì độ lệch chuẩn càng nhỏ và ngược lại
- Với mỗi mẫu số liệu: khoảng biến thiên = giá trị lớn nhất - giá trị nhỏ nhất
Lời giải chi tiết
a) Độ lệch chuẩn của mẫu số liệu A lớn hơn mẫu số liệu B
b) Ta có: giá trị nhỏ nhất của mẫu A là 1, giá trị nhỏ nhất của mẫu B là 2 và giá trị lớn nhất của cả hai mẫu đều là 5.
Khoảng biến thiên của hai mẫu số liệu không như nhau
Bài 5.13 trang 80 sách bài tập Toán 10 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ và ứng dụng trong hình học. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố sau:
Dưới đây là lời giải chi tiết bài 5.13 trang 80 sách bài tập Toán 10 Kết nối tri thức. (Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải, công thức sử dụng và giải thích rõ ràng từng bước. Ví dụ:)
Ví dụ lời giải (chỉ mang tính minh họa):
Giả sử bài toán yêu cầu tính độ dài của vectơ AB, với A(x1, y1) và B(x2, y2). Ta có công thức tính độ dài vectơ AB như sau:
|AB| = √((x2 - x1)² + (y2 - y1)²)
Thay các giá trị x1, y1, x2, y2 vào công thức, ta sẽ tính được độ dài của vectơ AB.
Ngoài bài 5.13, sách bài tập Toán 10 Kết nối tri thức còn có nhiều bài tập tương tự về vectơ và ứng dụng trong hình học. Dưới đây là một số dạng bài tập thường gặp:
Để giải các bài tập về vectơ một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Bài 5.13 trang 80 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
Hãy luyện tập thêm nhiều bài tập tương tự để nắm vững kiến thức và kỹ năng về vectơ nhé!