Bài 6.5 trang 8 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 6.5 trang 8, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trong một cuộc thi chạy 100m, có ba học sinh dự thi. Biểu đồ trên Hình 6.9 mô tả quãng đường chạy được y (m) theo thời gian t (s) của mỗi học sinh.
Đề bài
Trong một cuộc thi chạy 100m, có ba học sinh dự thi. Biểu đồ trên Hình 6.9 mô tả quãng đường chạy được y (m) theo thời gian t (s) của mỗi học sinh.
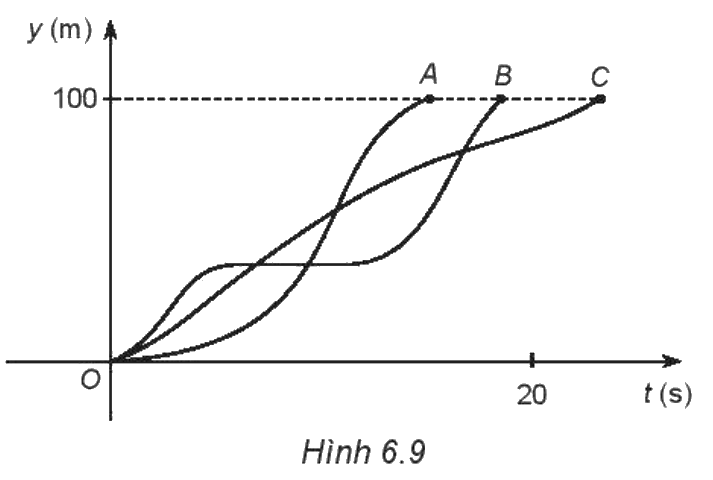
a) Đường biểu diễn quãng đường chạy được của mỗi học sinh có là đồ thị hàm số hay không?
b) Học sinh nào về đích đầu tiên? Hãy cho biết ba học sinh đó có chạy hết quãng đường thi theo quy định hay không.
Phương pháp giải - Xem chi tiết
Bước 1: Dựa vào định nghĩa hàm số để xét xem các đường biểu diễn quãng đường chạy được của mỗi học sinh có là đồ thị hàm số hay không.
Bước 2: Xét y = 100, so sánh từng giá trị x tương ứng. Giá trị x nào nhỏ hơn thì thời gian ngắn hơn, nghĩa là học sinh đó về đích nhanh hơn.
Bước 3: Dựa vào đồ thị kết luận ba học sinh đó có chạy hết quãng đường thi theo quy định hay không.
Lời giải chi tiết
a) Dựa vào đồ thị ta thấy với mỗi giá trị x của từng đường cong chỉ cho duy nhất một giá trị y tương ứng. Do đó đường biểu diễn quãng đường chạy được của mỗi học sinh là đồ thị hàm số
b) Xét y = 100 ta thấy xA < xB < xC. Do đó thời gian chạy của học sinh A là ngắn nhất nên học sinh A về đích đầu tiên và cả ba học sinh đều chạy hết quãng đường thi theo quy định.
Bài 6.5 trang 8 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập thuộc chương vectơ trong hình học. Bài tập này thường yêu cầu học sinh áp dụng các kiến thức về phép cộng, trừ vectơ, tích của một số với vectơ, và các tính chất của vectơ để giải quyết các bài toán liên quan đến vị trí tương đối của các điểm, chứng minh đẳng thức vectơ, hoặc tính độ dài của vectơ.
Thông thường, bài tập 6.5 sẽ bao gồm các dạng bài sau:
Để giải bài 6.5 trang 8 một cách hiệu quả, học sinh cần:
Dưới đây là ví dụ về cách giải một dạng bài tập thường gặp trong bài 6.5:
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2
Lời giải:
Vì M là trung điểm của BC, ta có: overrightarrow{BM} =overrightarrow{MC}. Do đó, overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM} =overrightarrow{AB} +overrightarrow{MC}. Mặt khác, overrightarrow{AC} =overrightarrow{AM} +overrightarrow{MC}, suy ra overrightarrow{MC} =overrightarrow{AC} -overrightarrow{AM}. Thay vào phương trình trên, ta được: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC} -overrightarrow{AM}. Từ đó, 2overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC}, hay overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 (đpcm).
Để học tốt và giải bài tập vectơ hiệu quả, bạn có thể tham khảo một số mẹo sau:
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để học toán 10 hiệu quả và đạt kết quả cao!