Bài 6.46 trang 24 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.46 trang 24 Sách bài tập Toán 10 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức
Đề bài
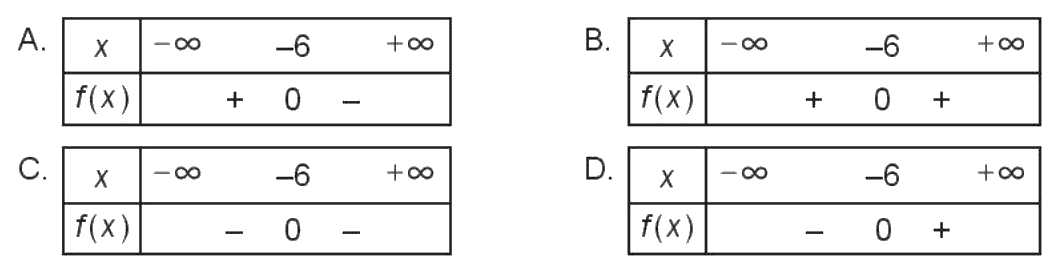
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức \(f(x) = {x^2} + 12x + 36\)?
Lời giải chi tiết
Tam thức bậc hai \(f(x) = {x^2} + 12x + 36\) có a = 1 > 0, ∆’ = 0 và có nghiệm kép x = -6 nên \({x^2} + 12x + 36\) > 0 \(\forall x \ne - 6\)
\( \Rightarrow \) Chọn B
Bài 6.46 trang 24 Sách bài tập Toán 10 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Nội dung bài tập 6.46: Bài tập yêu cầu học sinh chứng minh một đẳng thức vectơ liên quan đến các điểm và vectơ trong một hình học cụ thể. Để giải bài tập này, học sinh cần:
Lời giải chi tiết bài 6.46:
(Phần này sẽ chứa lời giải chi tiết, bao gồm các bước giải, giải thích rõ ràng và các ví dụ minh họa. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.)
Ví dụ minh họa:
Giả sử ta có tam giác ABC, với M là trung điểm của BC. Ta cần chứng minh rằng: MA = MB + MC. Để chứng minh đẳng thức này, ta có thể sử dụng quy tắc cộng vectơ. Theo quy tắc cộng vectơ, ta có: MB + MC = 2MA. Do đó, MA = MB + MC.
Mở rộng kiến thức:
Ngoài bài tập 6.46, còn rất nhiều bài tập khác liên quan đến vectơ trong chương trình Toán 10. Để nắm vững kiến thức về vectơ, học sinh cần luyện tập thường xuyên và tìm hiểu thêm các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp đầy đủ các bài giải, lý thuyết và bài tập về vectơ, giúp học sinh học Toán 10 hiệu quả.
Lưu ý khi giải bài tập về vectơ:
Tổng kết:
Bài 6.46 trang 24 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về vectơ. Hy vọng với lời giải chi tiết và dễ hiểu mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
Các bài tập tương tự: