Bài 4.20 trang 55 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập này một cách hiệu quả.
Cho tam giác ABC
Đề bài
Cho tam giác \(ABC.\)
a) Tìm điểm \(K\) thỏa mãn \(\overrightarrow {KA} + 2\overrightarrow {KB} + 3\overrightarrow {KC} = \overrightarrow 0 \)
b) Tìm tập hợp các điểm \(M\) thỏa mãn \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB} - \overrightarrow {MC} } \right|\)
Lời giải chi tiết
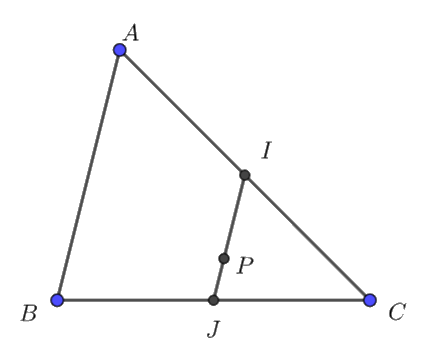
a) Giả sử tìm được điểm \(K\) thỏa mãn \(\overrightarrow {KA} + 2\overrightarrow {KB} + 3\overrightarrow {KC} = \overrightarrow 0 \)
Gọi \(I\) là trung điểm của \(AC\), \(J\) là trung điểm của \(BC\).
Ta có: \(\overrightarrow {KA} + 2\overrightarrow {KB} + 3\overrightarrow {KC} = \left( {\overrightarrow {KA} + \overrightarrow {KC} } \right) + 2\left( {\overrightarrow {KB} + \overrightarrow {KC} } \right) = 2\overrightarrow {KI} + 4\overrightarrow {KJ} \) (1)
Lấy điểm \(P\) trên cạnh \(IJ\) sao cho \(\overrightarrow {PI} + 2\overrightarrow {PJ} = \overrightarrow 0 \)
Ta có: \(2\overrightarrow {KI} + 4\overrightarrow {KJ} = 2\left( {\overrightarrow {KP} + \overrightarrow {PI} } \right) + 4\left( {\overrightarrow {KP} + \overrightarrow {PJ} } \right) = 6\overrightarrow {KP} \) (2)
Từ (1) và (2) \( \Rightarrow \) \(\overrightarrow {KA} + 2\overrightarrow {KB} + 3\overrightarrow {KC} = 6\overrightarrow {KP} \)
Mặt khác \(\overrightarrow {KA} + 2\overrightarrow {KB} + 3\overrightarrow {KC} = \overrightarrow 0 \)
\( \Rightarrow \) \(6\overrightarrow {KP} = \overrightarrow 0 \) \( \Leftrightarrow \) \(K \equiv P\)
Vậy điểm \(K\) thuộc cạnh \(IJ\) sao cho \(\overrightarrow {KI} + 2\overrightarrow {KJ} = \overrightarrow 0 \)
b) Ta có: \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB} - \overrightarrow {MC} } \right|\)
\( \Leftrightarrow \,\,\left| {6\overrightarrow {MP} } \right| = \left| {\overrightarrow {CB} } \right|\,\, \Leftrightarrow \,\,MP = \frac{1}{6}BC\)
\( \Rightarrow \) tập hợp điểm \(M\) cần tìm là đường tròn tâm \(P\), bán kính bằng \(\frac{{BC}}{6}\).
Bài 4.20 trang 55 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ về vectơ, các phép toán vectơ và cách áp dụng chúng vào giải quyết vấn đề.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho tam giác ABC, tìm điểm M sao cho...)
Để giải bài 4.20 trang 55, chúng ta cần thực hiện các bước sau:
(Ví dụ cụ thể với các số liệu và cách giải chi tiết sẽ được trình bày ở đây. Bao gồm các bước tính toán, giải thích rõ ràng từng bước để học sinh dễ hiểu.)
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, bạn có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về vectơ, bạn cần lưu ý những điều sau:
Bài 4.20 trang 55 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán ứng dụng thực tế về vectơ. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các bạn học sinh sẽ nắm vững kiến thức và tự tin giải quyết bài tập này một cách hiệu quả.