Bài 1.10 trang 11 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh phải hiểu rõ khái niệm tập hợp, các ký hiệu và cách xác định một tập hợp.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.10 trang 11 sách bài tập Toán 10 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai tập hợp A,B được mô tả bởi biểu đồ ven như sau:
Đề bài
Cho hai tập hợp \(A,\,\,B\) được mô tả bởi biểu đồ ven như sau:
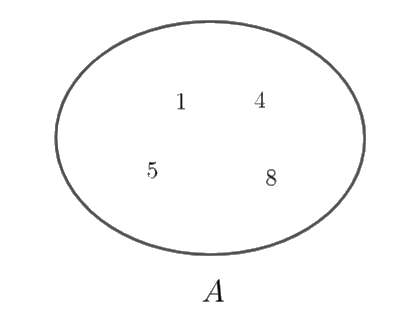
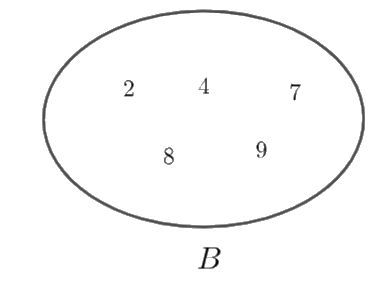
a) Hãy chỉ ra các phần tử của tập hợp \(A,\) tập hợp \(B.\)
b) Tính \(n\left( {A \cup B} \right)\)
c) Hãy chỉ ra các phần tử thuộc tập hợp \(A\) mà không thuộc tập hợp \(B.\)
d) Hãy chỉ ra các phần tử thuộc tập hợp \(B\) mà không thuộc tập hợp \(A.\)
Phương pháp giải - Xem chi tiết
- Viết các phần tử cửa tập hợp A, tập hợp B dưới dạng liệt kê
- \(A \cup B\) là tập hợp các phần tử hoặc thuộc tập hợp A hoặc thuộc tập hợp B
- Viết các phần tử của tập hợp A những không thuộc tập hợp B và ngược lại
Lời giải chi tiết
a) \(A = \left\{ {1;4;5;8} \right\},\quad B = \left\{ {2;4;7;8;9} \right\}\)
b) \(A \cup B = \left\{ {1;2;4;5;7;8;9} \right\}\,\, \Rightarrow \,\,n\left( {A \cup B} \right) = 7.\)
c) \(A\backslash B = \left\{ {1;5} \right\}\)
d) \(B\backslash A = \left\{ {2;7;9} \right\}\)
Bài 1.10 trang 11 sách bài tập Toán 10 Kết nối tri thức yêu cầu chúng ta xác định các tập hợp dựa trên các điều kiện cho trước. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về tập hợp, bao gồm:
Bài 1.10 thường bao gồm các câu hỏi yêu cầu xác định các tập hợp con, hợp, giao, hiệu của các tập hợp cho trước. Ví dụ:
Cho hai tập hợp A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Hãy tìm:
Để giải bài tập này, chúng ta cần áp dụng các công thức và quy tắc sau:
Áp dụng vào ví dụ trên, ta có:
Ngoài bài 1.10, sách bài tập Toán 10 Kết nối tri thức còn có nhiều bài tập tương tự về tập hợp. Các bài tập này thường yêu cầu:
Để giải bài tập về tập hợp một cách hiệu quả, bạn nên:
Tập hợp là một khái niệm cơ bản trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như khoa học máy tính, thống kê, và logic. Việc nắm vững kiến thức về tập hợp sẽ giúp bạn hiểu sâu hơn về các khái niệm toán học khác và giải quyết các bài toán phức tạp một cách hiệu quả.
Bài 1.10 trang 11 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về tập hợp. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 10.