Bài 8.33 trang 60 SBT Toán 10 Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.33 trang 60 SBT Toán 10 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
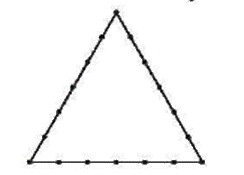
Trong hình sau đây, mỗi cạnh của tam giác đều được chia thành 6 đoạn | thẳng bằng nhau bởi 5 điểm nằm bên trong cùng với hai đầu mút. Hỏi có bao nhiêu tam giác có đỉnh là các chấm điểm ở trong hình:
Đề bài
Trong hình sau đây, mỗi cạnh của tam giác đều được chia thành 6 đoạn | thẳng bằng nhau bởi 5 điểm nằm bên trong cùng với hai đầu mút. Hỏi có bao nhiêu tam giác có đỉnh là các chấm điểm ở trong hình:
Phương pháp giải - Xem chi tiết
Áp dụng công thức tổ hợp và quy tắc cộng.
Lời giải chi tiết
Tổng số chấm điểm trong hình là 18.
Mỗi tam giác được tạo thành từ 3 điểm không thẳng hàng. Ta tính số cách chọn ra 3 điểm không thẳng hàng bằng số cách lấy số cách chọn ra 3 điểm trừ đi cách chọn ra 3 điểm thẳng hàng.
Số cách chọn ra 3 điểm từ 18 điểm là:
\(C_{18}^3 = 816\) cách
Chọn ra 3 điểm thẳng hàng bằng cách chọn ra 3 điểm trên cùng 1 cạnh.
Mỗi cạnh có 7 điểm do đó có số cách chọn ra 3 điểm từ 1 cạnh là \(C_7^3 = 35\)cách
Số cách chọn ra 3 điểm thẳng hàng là 35+ 35+ 35= 105 cách
Vậy số tam giác cần tìm là: 816 - 105= 711.
Bài 8.33 trang 60 SBT Toán 10 Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Dưới đây là đề bài chi tiết:
Cho hình vuông ABCD có cạnh bằng a. Gọi M là trung điểm của cạnh BC. Tính AM.AD.
Để giải bài toán này, ta thực hiện các bước sau:
Vậy, AM.AD = a2/2.
Bài toán này yêu cầu học sinh vận dụng kiến thức về vectơ và tích vô hướng để giải quyết. Việc chọn hệ tọa độ phù hợp là rất quan trọng để đơn giản hóa bài toán. Ngoài ra, học sinh có thể giải bài toán bằng phương pháp hình học, tuy nhiên phương pháp tọa độ thường nhanh và chính xác hơn.
Để hiểu rõ hơn về vectơ và tích vô hướng, các em có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và sách bài tập Toán 10 Kết nối tri thức. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến trên giaitoan.edu.vn.
Dưới đây là một số bài tập tương tự để các em luyện tập:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài 8.33 trang 60 SBT Toán 10 Kết nối tri thức và tự tin giải các bài tập tương tự. Chúc các em học tốt!
| Khái niệm | Công thức |
|---|---|
| Tích vô hướng | a.b = |a||b|cos(θ) |
| Tính chất tích vô hướng | a.b = b.a, (ka).b = k(a.b) |