Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách giải bài 2.3 trang 18 trong sách bài tập Toán 10 - Kết nối tri thức với cuộc sống.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các giải thích rõ ràng để giúp bạn nắm vững kiến thức và kỹ năng cần thiết.
Xác định một bất phương trình bậc nhất hai ẩn nhân nửa mặt phẳng bờ là đường thẳng d (miền không bị gạch) làm miền nghiệm.
Đề bài
Xác định một bất phương trình bậc nhất hai ẩn nhân nửa mặt phẳng bờ là đường thẳng \(d\) (miền không bị gạch) làm miền nghiệm.
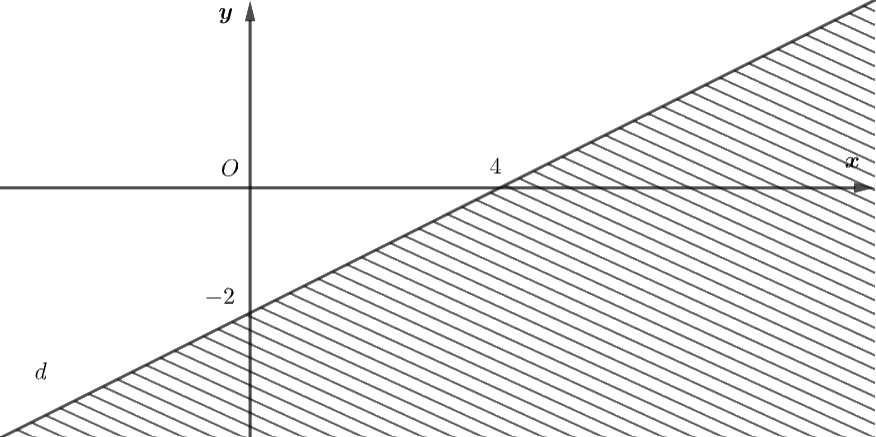
Phương pháp giải - Xem chi tiết
- Gọi đường thẳng \(d\) cần tìm là: \(d:y = ax + b,\,\,\left( {a \ne 0} \right).\)
- Xác định đường thẳng \(d\)
- Từ miền nghiệm của bất phương trình, kết luận bất phương trình cần tìm.
Lời giải chi tiết
Gọi đường thẳng \(d\) cần tìm là: \(d:y = ax + b,\,\,\left( {a \ne 0} \right).\)
Nhìn vào độ thị thì đường thẳng \(d\) đi qua điểm \(A\left( {4;0} \right)\) và \(B\left( {0; - 2} \right)\)
Thay điểm \(A\left( {4;0} \right)\) vào \(d\) ta được: \(4a + b = 0.\)
Thay điểm \(B\left( {0; - 2} \right)\) vào \(d\) ta được: \(0a + b = - 2\,\, \Rightarrow \,\,b = - 2\)
Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{4a + b = 0}\\{b = - 2}\end{array}} \right.\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = \frac{1}{2}}\\{b = - 2}\end{array}} \right.\)
\( \Rightarrow \,\,d:y = \frac{1}{2}x - 2\,\, \Leftrightarrow \,\,x - 2y = 4.\)
Vì miền nghiệm của đồ thị là nửa mặt phẳng bờ \(d\) chứa điểm \(O\) nên bất phương trình cần tìm là: \(x - 2y \le 4\)
Bài 2.3 trang 18 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống thường xoay quanh các chủ đề về tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của tập hợp. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và định nghĩa liên quan.
Trước khi đi vào giải bài tập cụ thể, hãy cùng ôn lại một số kiến thức cơ bản về tập hợp:
Để giải bài 2.3 trang 18, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu chúng ta thực hiện một hoặc nhiều phép toán trên các tập hợp cho trước. Ví dụ:
Cho hai tập hợp A = {1, 2, 3} và B = {2, 4, 5}. Hãy tìm:
a) A ∪ B (hợp của A và B):
Hợp của hai tập hợp A và B là tập hợp chứa tất cả các phần tử thuộc A hoặc thuộc B (hoặc cả hai).
A ∪ B = {1, 2, 3, 4, 5}
b) A ∩ B (giao của A và B):Giao của hai tập hợp A và B là tập hợp chứa tất cả các phần tử thuộc cả A và B.
A ∩ B = {2}
c) A \ B (hiệu của A và B):Hiệu của hai tập hợp A và B là tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B.
A \ B = {1, 3}
Ngoài bài 2.3 trang 18, sách bài tập Toán 10 - Kết nối tri thức với cuộc sống còn nhiều bài tập tương tự về tập hợp. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để nắm vững kiến thức về tập hợp và các phép toán trên tập hợp, bạn nên luyện tập thêm các bài tập khác trong sách bài tập và các tài liệu tham khảo khác. Bạn cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học Toán 10 để được hướng dẫn chi tiết hơn.
| Phép toán | Công thức |
|---|---|
| Hợp (∪) | A ∪ B = {x | x ∈ A hoặc x ∈ B} |
| Giao (∩) | A ∩ B = {x | x ∈ A và x ∈ B} |
| Hiệu (\) | A \ B = {x | x ∈ A và x ∉ B} |
| Bù (C) | CA = {x | x ∈ Ω và x ∉ A} |
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 2.3 trang 18 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống. Chúc bạn học tập tốt!