Bài 3.19 trang 40 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.19 trang 40, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trên mặt phẳng tọa độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho
Đề bài
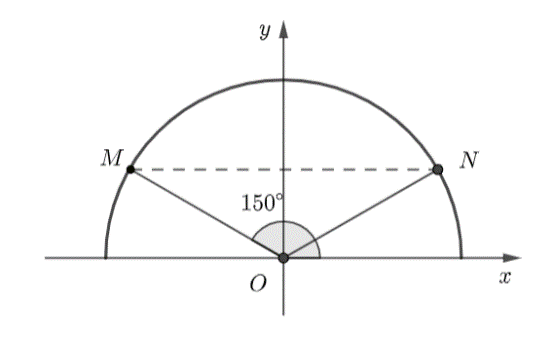
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {150^ \circ }.\) \(N\) là điểm đối xứng với \(M\) qua trục tung. Giá trị của \(\tan \widehat {xON}\) bằng:
A. \(\frac{1}{{\sqrt 3 }}.\)
B. \( - \frac{1}{{\sqrt 3 }}.\)
C. \(\sqrt 3 .\)
D. \( - \sqrt 3 .\)
Phương pháp giải - Xem chi tiết
- Vẽ hình trên mặt phẳng tọa độ \(Oxy.\)
- Tính \(\widehat {xON}\) và \(\tan \widehat {xON}\)
Lời giải chi tiết
Ta có: \(\widehat {xON} = {180^ \circ } - {150^ \circ } = {30^ \circ }.\)
\( \Rightarrow \,\,\tan \widehat {xON} = \tan {30^ \circ } = \frac{{\sqrt 3 }}{3}.\)
Chọn A.
Bài 3.19 trang 40 sách bài tập Toán 10 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ trong mặt phẳng. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi đi vào giải bài toán cụ thể, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố sau:
Dưới đây là lời giải chi tiết bài 3.19 trang 40 sách bài tập Toán 10 Kết nối tri thức:
(a) Tìm tọa độ của vectơ AB.
Giả sử A(xA, yA) và B(xB, yB). Khi đó, vectơ AB có tọa độ là:
AB = (xB - xA, yB - yA)
(b) Tìm tọa độ của vectơ AC.
Tương tự như trên, nếu C(xC, yC), thì vectơ AC có tọa độ là:
AC = (xC - xA, yC - yA)
(c) Tính tích vô hướng của hai vectơ AB và AC.
Tích vô hướng của hai vectơ AB = (x1, y1) và AC = (x2, y2) được tính như sau:
AB . AC = x1x2 + y1y2
Giả sử A(1, 2), B(3, 4), C(5, 6). Hãy tính tọa độ của vectơ AB, AC và tích vô hướng của chúng.
Giải:
Khi giải các bài toán về vectơ, cần chú ý các điểm sau:
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách bài tập Toán 10 Kết nối tri thức. Ngoài ra, bạn có thể tìm kiếm các bài tập trực tuyến để luyện tập thêm.
Bài 3.19 trang 40 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về vectơ và các phép toán vectơ. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin giải quyết bài toán này một cách hiệu quả.