Bài 3.12 trang 39 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.12 trang 39, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Một cây cổ thụ mạc thẳng đứng bên lề một con dốc có độ dốc 10 so với phương nằm ngang. Từ một điểm dưới chân dốc, cách gốc cây 31 m người ta nhìn đỉnh ngọn cây dưới một góc 40 so với phương nằm ngang. Hãy tính chiều cao của cây.
Đề bài
Một cây cổ thụ mạc thẳng đứng bên lề một con dốc có độ dốc \({10^ \circ }\) so với phương nằm ngang. Từ một điểm dưới chân dốc, cách gốc cây 31 m người ta nhìn đỉnh ngọn cây dưới một góc \({40^ \circ }\) so với phương nằm ngang. Hãy tính chiều cao của cây.
Phương pháp giải - Xem chi tiết
- Tính \(\widehat {BAC}\) và \(\widehat {ACB}\)
- Áp dụng định lý sin, tính cạnh \(BC:\frac{{BC}}{{\sin BAC}} = \frac{{AB}}{{\sin ACB}}\)
Lời giải chi tiết
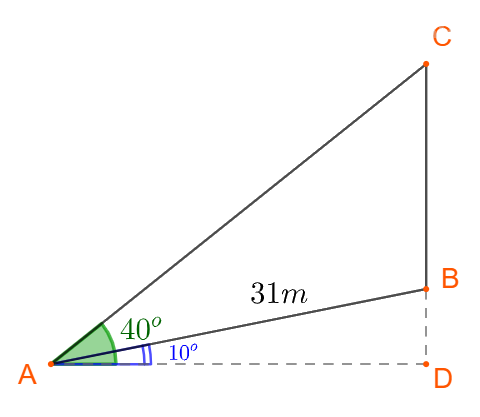
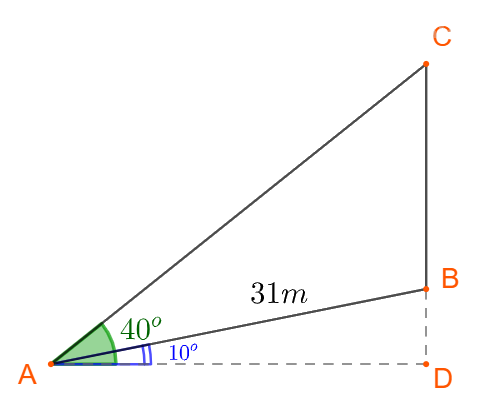
Giả sử con dốc là AB, gốc cây đặt tại B, chiều cao cây cổ thụ là đoạn CB.
Khi đó ta có: \( \widehat {BAD} = {10^ \circ },\, \widehat {CAD} = {40^ \circ }\) và \(AB=31m\)
Xét \(\Delta ADC\) vuông tại \(D\) có: \(\widehat {ACB} = {90^ \circ } - \widehat {DAC} = {90^ \circ } - {40^ \circ } = {50^ \circ }.\)
Ta có: \(\widehat {CAB} = \widehat {DAC} - \widehat {DAB} = {40^ \circ } - {10^ \circ } = {30^ \circ }.\)
Chiều cao của cây là:
Áp dụng định lý sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin BAC}} = \frac{{AB}}{{\sin ACB}}\,\, \Rightarrow \,\,BC = \frac{{AB.\sin BAC}}{{\sin ACB}}\\ \Rightarrow \,\,BC = \frac{{31.\sin {{30}^ \circ }}}{{\sin {{50}^ \circ }}} \approx 20,23\,\,m\end{array}\)
Bài 3.12 trang 39 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vectơ và ứng dụng trong hình học. Để giải bài toán này, chúng ta cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Nội dung bài toán: (Giả sử bài toán cụ thể là tìm tọa độ điểm D sao cho ABCD là hình bình hành, với A, B, C có tọa độ cho trước)
Để giải bài toán này, chúng ta có thể sử dụng tính chất của hình bình hành: vectơ AB = vectơ DC. Từ đó, ta có thể tìm được tọa độ của điểm D.
Ví dụ minh họa:
Giả sử A(1; 2), B(3; 4), C(5; 1). Tìm tọa độ điểm D sao cho ABCD là hình bình hành.
Giải:
Mở rộng kiến thức:
Ngoài việc giải bài tập cụ thể, các em học sinh nên tìm hiểu thêm về các ứng dụng của vectơ trong hình học, chẳng hạn như:
Việc nắm vững kiến thức về vectơ sẽ giúp các em học sinh giải quyết các bài toán hình học một cách hiệu quả và chính xác hơn.
Giaitoan.edu.vn hy vọng với lời giải chi tiết và phương pháp giải rõ ràng trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 10 Kết nối tri thức. Chúc các em học tập tốt!
Các bài tập tương tự: