Bài 2.5 trang 19 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.5 trang 19 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một cửa hàng bán lẻ bán hai loại hạt cà phê. Loại thứ nhất với giá 140 nghìn đồng/kg và loại thứ hai với giá 180 nghìn đồng/kg. Cửa hàng trộn x kg loại thứ nhất và y loại thứ hai sao cho hạt cà phê đã trộn có giá không quá 170 nghìn đồng/kg.
Đề bài
Một cửa hàng bán lẻ bán hai loại hạt cà phê. Loại thứ nhất với giá 140 nghìn đồng/kg và loại thứ hai với giá 180 nghìn đồng/kg. Cửa hàng trộn x kg loại thứ nhất và y loại thứ hai sao cho hạt cà phê đã trộn có giá không quá 170 nghìn đồng/kg.
a) Viết bất phương trình bậc nhất hai ẩn \(x;\,\,y\) thỏa mãn điều kiện đề bài.
b) Biểu diễn miền nghiệm của bất phương trình tìm được ở câu a trên mặt phẳng tọa độ.
Phương pháp giải - Xem chi tiết
- Viết bất phương trình bậc nhất thỏa mãn bài toán trên.
- Xác định miền nghiệm của bất phương trình.
Lời giải chi tiết
a) Gọi \(x\) và \(y\) lần lượt là số kg cà phê loại thứ nhất và loại thứ 2.
Ta có: Loại thứ nhất với giá 140 nghìn đồng/kg và loại thứ hai với giá 180 nghìn đồng/kg nên ta có: \(140x + 180y.\)
Theo đề bài, ta có: \(140x + 180y \le 170\left( {x + y} \right)\)
\(\begin{array}{l} \Leftrightarrow \,\,140x + 180y \le 170x + 170y\\ \Leftrightarrow \,\, - 30x + 10y \le 0\\ \Leftrightarrow \,\,3x - y \ge 0.\end{array}\)
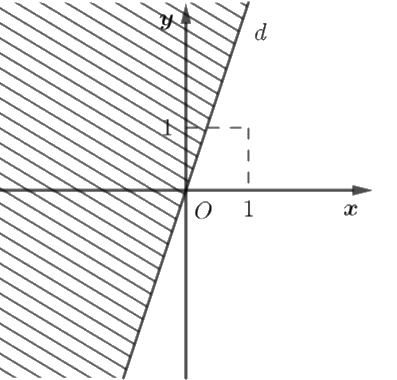
b) Ta biểu diễn miền nghiệm của bất phương trình như sau:
Vẽ đường thẳng \(d:3x - y = 0\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn \(A\left( {1;1} \right)\) là điểm không thuộc đường thẳng \(d\) và thay vào biểu thức \(3x - y,\) ta được \(3.1 - 1 = 2 > 0.\)
Do đó, miền nghiệm của bất phương trình \(3x - y \ge 0\) là nửa mặt phẳng bờ \(d\) và chứa điểm \(A\left( {1;1} \right)\).
Bài 2.5 trang 19 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập thuộc chương vectơ trong hình học. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Dưới đây là hướng dẫn giải chi tiết bài 2.5 trang 19 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống:
Đề bài: (Giả sử đề bài là: Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo vectơ AB và AC.)
Lời giải:
Áp dụng quy tắc trung điểm, ta có:
AM = (AB + AC) / 2
Vậy, vectơ AM được biểu diễn qua vectơ AB và AC là AM = (AB + AC) / 2.
Bài toán này yêu cầu học sinh vận dụng quy tắc trung điểm để biểu diễn một vectơ qua hai vectơ khác. Quy tắc trung điểm là một công cụ quan trọng trong hình học vectơ, giúp giải quyết nhiều bài toán liên quan đến trung điểm, trọng tâm, đường trung bình của tam giác, và các khái niệm tương tự.
Ngoài bài 2.5 trang 19, sách bài tập Toán 10 - Kết nối tri thức với cuộc sống còn có nhiều bài tập tương tự về vectơ. Một số dạng bài tập thường gặp bao gồm:
Để giải bài tập vectơ hiệu quả, học sinh nên:
Vectơ không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng trong thực tế, chẳng hạn như:
Để củng cố kiến thức về vectơ, học sinh nên luyện tập thêm các bài tập trong sách giáo khoa, sách bài tập, và các nguồn tài liệu khác. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng về vectơ, giúp học sinh rèn luyện kỹ năng và nâng cao trình độ.
Bài 2.5 trang 19 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh nắm vững kiến thức về vectơ. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán 10.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!