Bài 3.10 trang 39 sách bài tập Toán 10 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự. Hãy cùng khám phá!
a) Tính khoảng cách từ vị trí xuất phát từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị đo ki lô mét).
Đề bài
Một tàu các xuất phát từ đảo \(A,\) chạy 50 km theo hướng \(N{24^ \circ }E\) đến đảo \(B\) để lấy thêm ngư cụ, rồi chuyển hướng \(N{36^ \circ }W\) chạy tiếp 130 km đến ngư trường \(C.\)
a) Tính khoảng cách từ vị trí xuất phát từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị đo ki lô mét).
b) Tìm hướng từ A đến C ( đơn vị đến hàng đơn vị, theo đơn vị độ).
Phương pháp giải - Xem chi tiết
- Tính \(\widehat B\)
- Áp dụng định lý cosin để tính độ dài \(AC:\) \(A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos B\)
- Tính \(\widehat {CAB}\) dựa vào định lý sin \(\frac{{CB}}{{\sin CAB}} = \frac{{AC}}{{\sin ABC}}\)
- Tính góc AC chếch về hương tây
Lời giải chi tiết
Ta có: \(\widehat B = \left( {{{90}^ \circ } - {{36}^ \circ }} \right) + \left( {{{90}^ \circ } - {{24}^ \circ }} \right) = {120^ \circ }.\)
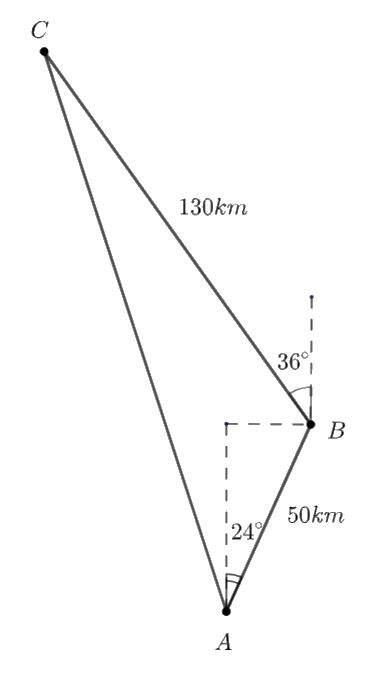
a) Độ dài đoạn thẳng AC là:
Áp dụng định lý cosin, ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos B\\A{C^2} = {50^2} + {130^2} - 2.50.130.\cos {120^ \circ }\\A{C^2} = 2500 + 16900 + 6500 = 25900\\ \Rightarrow \,\,AC = \sqrt {25900} = 10\sqrt {259} \approx 161\,\,km\end{array}\)
b) Áp dụng định lý sin, ta có:
\(\begin{array}{l}\frac{{CB}}{{\sin CAB}} = \frac{{AC}}{{\sin ABC}}\,\, \Rightarrow \,\,\frac{{130}}{{\sin CAB}} = \frac{{161}}{{\sin {{120}^ \circ }}}\\ \Rightarrow \,\,\sin CAB = \frac{{130.\sin {{120}^ \circ }}}{{161}} \approx 0,6993\\ \Rightarrow \,\,\widehat {CAB} \approx {44^ \circ }\end{array}\)
Góc AC chếch về hướng tây một góc \({44^ \circ } - {24^ \circ } = {20^ \circ }.\)
Vậy hướng từ A đến C là: \(N{20^ \circ }W\)
Bài 3.10 yêu cầu học sinh vận dụng kiến thức về vectơ, đặc biệt là các phép toán vectơ như cộng, trừ, nhân với một số thực, và tích vô hướng để giải quyết một bài toán hình học cụ thể. Bài toán thường liên quan đến việc chứng minh các đẳng thức vectơ, xác định vị trí tương đối của các điểm, hoặc tính độ dài đoạn thẳng, góc giữa hai vectơ.
Để giải bài 3.10, chúng ta cần phân tích kỹ đề bài, xác định các vectơ liên quan, và áp dụng các kiến thức đã học để tìm ra lời giải. Dưới đây là một ví dụ về cách giải bài 3.10 (lưu ý rằng nội dung cụ thể của bài toán có thể khác nhau tùy theo sách bài tập):
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2
Vì M là trung điểm của BC, ta có: overrightarrow{BM} =overrightarrow{MC}. Theo quy tắc trung điểm, ta có: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2. Vậy, đẳng thức được chứng minh.
Bài 3.10 trang 39 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng trong hình học. Bằng cách nắm vững các kiến thức cơ bản, áp dụng các quy tắc và tính chất của vectơ, và luyện tập thường xuyên, bạn có thể tự tin giải quyết bài tập này và các bài tập tương tự.