Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 2 trang 70 sách bài tập Toán 10 chương trình Kết nối tri thức với cuộc sống. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ bản chất của bài toán.
a) Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau: (left{ begin{array}{l}x ge 0\y ge 0\3x - 2y ge - 6\2x + y le 10end{array} right.) b) Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x;y)=2x +3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất)của F đạt được tại một trong các đỉnh của miền đa giác D.
Đề bài
a) Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất
hai ẩn sau:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\3x - 2y \ge - 6\\2x + y \le 10\end{array} \right.\)
b) Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x;y)=2x +3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất)của F đạt được tại một trong các đỉnh của miền đa giác D.
Phương pháp giải - Xem chi tiết
- Xác định miền nghiệm của hệ bất phương trình (là một miền đa giác).
- Xác định tọa độ các đỉnh của đa giác.
- Tính giá trị của biểu thức f=2x+3y với (x,y) là tọa độ các đỉnh của đa giác sau đó so sánh để tìm ra giá trị nhỏ nhất.
Lời giải chi tiết
a) - Bước 1: Trục Oy có phương trình x = 0 và điểm (1; 0) thoả mãn 1 > 0. Do đó miền nghiệm của bất phương trình là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (miền không bị gạch).
- Bước 2: Trục Ox có phương trình y = 0 và điểm (0; 1) thoả mãn 1> 0. Do đó miền nghiệm của bất phương trình là nửa mặt phẳng bờ Ox chứa điểm (0; 1) (miền không bị gạch).
- Bước 3: Vẽ đường thẳng : 3x - 2y = -6. Lấy điểm O(0;0) không thuộc , và thay x = 0, y = 0 vào biểu thức 3x - 2y ta được: 3.0 – 2.0 = 0>-6. Do đó miền nghiệm của bất phương trình 3x - 2y = -6 là nửa mặt phẳng bờ, chứa điểm O(0; 0) (miền không bị gạch).
- Bước 4: Vẽ đường thẳng : 2x + y = 10 và điểm O(0; 0) thoả mãn 2.0 + 0 =0 < 10. Do đó miền nghiệm của bất phương trình 2x + y = 10 là nửa mặt phẳng bờ chứa điểm O(0, 0) (miền không bị gạch).
Vậy miền nghiệm D của hệ là miền tứ giác OABC (miền không bị gạch), trong đó A(0; 3), B(2; 6), C(5; 0), như hình vẽ sau:
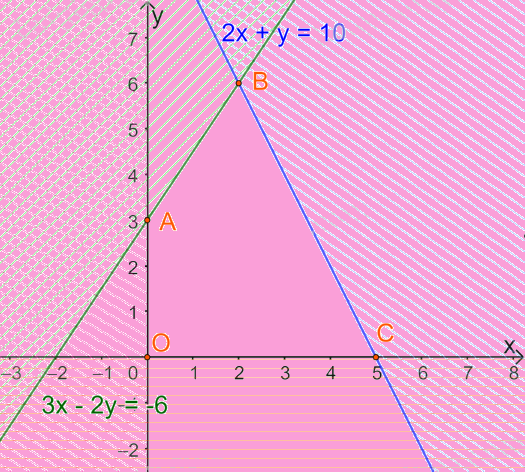
b) Ta có: F(0;0)=2.0 + 3.0= 0; F(0;3)=2.0 + 3.3= 9
F(2;6)=2.2 + 3.6= 22; F(5;0)=2.5 + 3.0= 10
Vậy trên miền D: giá trị lớn nhất của biểu thức F(x;y)=2x +3y là 22 và giá trị nhỏ nhất của biểu thức F(x;y)=2x +3y là 0.
Bài 2 trang 70 sách bài tập Toán 10 Kết nối tri thức thuộc chương trình học về hàm số bậc hai. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về:
Trước khi bắt tay vào giải bài, hãy đọc kỹ đề bài và xác định rõ yêu cầu. Bài 2 trang 70 thường yêu cầu chúng ta:
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể. Giả sử bài toán yêu cầu chúng ta giải hàm số y = 2x2 - 4x + 1.
Trong hàm số y = 2x2 - 4x + 1, ta có:
Tọa độ đỉnh của parabol có dạng (x0; y0), với:
Vậy tọa độ đỉnh của parabol là (1; -1).
Trục đối xứng của parabol là đường thẳng x = x0 = 1.
Để vẽ đồ thị hàm số, ta cần xác định thêm một vài điểm thuộc đồ thị. Ví dụ:
Vẽ các điểm này trên hệ trục tọa độ và nối chúng lại bằng một đường cong parabol.
Tùy thuộc vào yêu cầu cụ thể của bài toán, chúng ta có thể sử dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế, chẳng hạn như tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số, hoặc tìm khoảng giá trị của x sao cho y thỏa mãn một điều kiện nào đó.
Để hiểu sâu hơn về hàm số bậc hai, bạn có thể tham khảo thêm các tài liệu sau:
Khi giải bài tập Toán, hãy luôn kiểm tra lại kết quả của mình để đảm bảo tính chính xác. Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè để được giúp đỡ.
Bài 2 trang 70 sách bài tập Toán 10 Kết nối tri thức là một bài toán quan trọng giúp bạn củng cố kiến thức về hàm số bậc hai. Hy vọng rằng với lời giải chi tiết và phương pháp tiếp cận mà chúng tôi đã trình bày, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.