Bài 2.25 trang 27 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập này một cách hiệu quả.
Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:
Đề bài
Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:
a) \(x + y \ge - 4.\) | b) \(2x - y \le 5.\) |
c) \(x + 2y < 0.\) | d) \( - x + 2y > 0.\) |
Phương pháp giải - Xem chi tiết
- Vẽ các đường thẳng trên cùng một mặt phẳng tọa độ \(Oxy.\)
- Xác định miền nghiệm của hệ bất phương trình trên.
Lời giải chi tiết
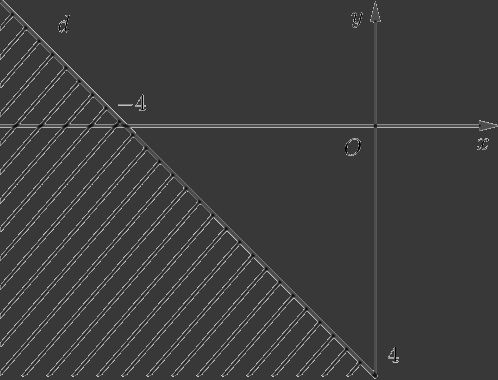
a) Xác định miền nghiệm của bất phương trình \(x + y \ge - 4.\)
Vẽ đường thẳng \(d:x + y = - 4\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn điểm \(O\left( {0;0} \right)\) không thuộc đường thẳng \(d\) và thay vào biểu thức \(x + y,\) ta được: \(0 + 0 = 0 > - 4\)
Do đó, miền nghiệm của hệ bất phương trình \(x + y \ge - 4\) là nửa mặt phẳng bờ \(d\) chứa gốc tọa độ \(O\left( {0;0} \right)\).
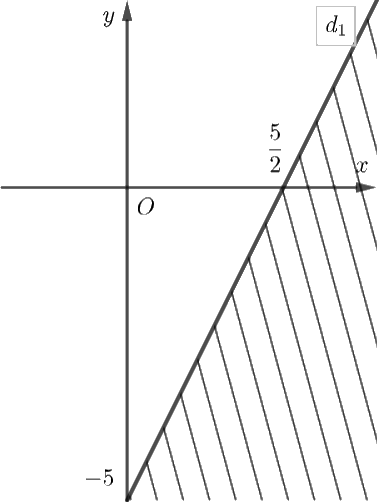
b) Xác định miền nghiệm của bất phương trình \(2x - y \le 5.\)
Vẽ đường thẳng \({d_1}:2x - y = 5\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn điểm \(O\left( {0;0} \right)\) không thuộc đường thẳng \({d_1}\) và thay vào biểu thức \(2x - y,\) ta được: \(2.0 - 0 = 0 < 5\).
Do đó, miền nghiệm của bất phương trình \(2x - y \le 5\) là nửa mặt phẳng bờ \({d_1}\) chứa gốc tọa độ \(O\left( {0;0} \right)\).
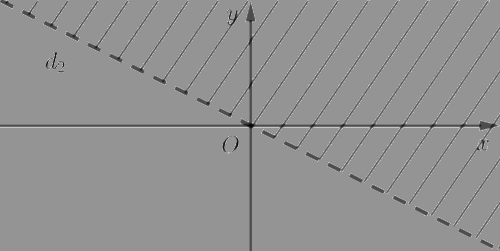
c) Xác định miền nghiệm của bất phương trình \(x + 2y < 0.\)
Vẽ đường thẳng \({d_2}:x + 2y = 0\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn điểm \(A\left( {1;0} \right)\) không thuộc đường thẳng \({d_2}\) và thay vào biểu thức \(x + 2y,\) ta được: \(1 + 2.0 = 1 > 0\).
Do đó, miền nghiệm của bất phương trình \(x + 2y < 0\) là nửa mặt phẳng bờ \({d_2}\) không chứa điểm \(A\left( {1;0} \right)\) nhưng bỏ đi đường thẳng \({d_2}\).
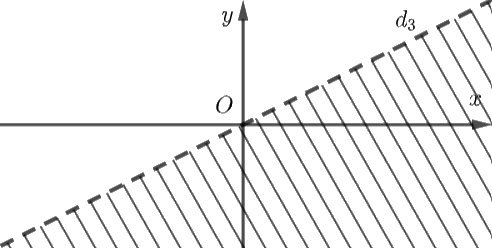
d) Xác định miền nghiệm của bất phương trình \( - x + 2y > 0.\)
Vẽ đường thẳng \({d_3}: - x + 2y = 0\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn điểm \(A\left( {1;1} \right)\) là điểm không thuộc đường thẳng \({d_3}\) và thay vào biểu thức \( - x + 2y,\) ta được: \( - 1 + 2.1 = - 1 + 2 = 1 > 0.\)
Do đó, miền nghiệm của bất phương trình \( - x + 2y > 0\) là nửa mặt phẳng bờ \({d_3}\) chứa điểm \(A\left( {1;1} \right)\).
Bài 2.25 trang 27 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế về vectơ. Để giải bài toán này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Trước khi đi vào giải bài toán cụ thể, chúng ta cần phân tích đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài 2.25 thường yêu cầu học sinh:
Dưới đây là lời giải chi tiết cho bài 2.25 trang 27 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, công thức sử dụng, và giải thích rõ ràng từng bước. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tính độ dài của một đoạn thẳng. Ta sẽ sử dụng công thức tính độ dài vectơ để giải quyết bài toán này. Cụ thể, nếu vectơ a = (x; y), thì độ dài của vectơ a được tính bằng công thức: |a| = √(x² + y²).
Ngoài bài 2.25, còn rất nhiều bài tập tương tự về vectơ trong sách bài tập Toán 10 - Kết nối tri thức với cuộc sống. Để nắm vững kiến thức và kỹ năng giải bài tập về vectơ, học sinh nên luyện tập thêm các bài tập sau:
Để giải bài tập về vectơ một cách hiệu quả, học sinh có thể tham khảo một số mẹo sau:
Vectơ có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài 2.25 trang 27 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải bài tập. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi cung cấp, các bạn học sinh sẽ tự tin hơn khi đối mặt với bài toán này và các bài toán tương tự.
Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị về toán học tại giaitoan.edu.vn!