Bài 4.53 trang 68 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.53 trang 68, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC có AB = 1,BC = 2
Đề bài
Cho tam giác \(ABC\) có \(AB = 1,\,\,BC = 2\) và \(\widehat {ABC} = {60^ \circ }.\) Tích vô hướng \(\overrightarrow {BC} .\overrightarrow {CA} \) bằng
A. \(\sqrt 3 \)
B. \( - \sqrt 3 \)
C. \(3\)
D. \( - 3\)
Phương pháp giải - Xem chi tiết
- Áp dụng định lý cosin để tính \(AC\): \(A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos \widehat {ABC}\)
- Áp dụng định lý sin để tính góc \(\widehat {ACB}\): \(\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{AC}}{{\sin \widehat {ABC}}}\)
- Áp dụng công thức tính tích vô hướng của \(\overrightarrow {BC} .\overrightarrow {CA} \)
Lời giải chi tiết
Gọi \(D\) là điểm đối xứng với \(B\) qua \(C\)
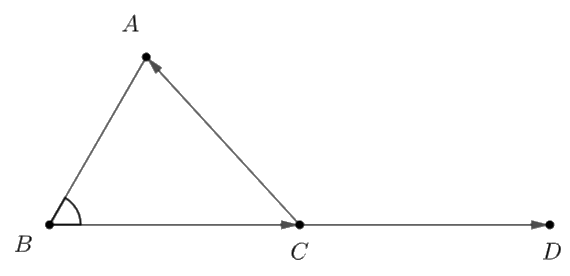
Áp dụng định lý cosin, ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos \widehat {ABC}\\ \Rightarrow \,\,A{C^2} = 1 + 4 - 2.1.2.\cos {60^ \circ } = 3\\ \Rightarrow \,\,AC = \sqrt 3 \end{array}\)
Áp dụng định lý sin, ta có:
\(\begin{array}{l}\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{AC}}{{\sin \widehat {ABC}}}\,\, \Leftrightarrow \,\,\frac{1}{{\sin \overrightarrow {ACB} }} = \frac{{\sqrt 3 }}{{\sin {{60}^ \circ }}}\\ \Leftrightarrow \,\,\sin \widehat {ACB} = \frac{{\sin {{60}^ \circ }}}{{\sqrt 3 }} = \frac{1}{2}\\ \Leftrightarrow \,\,\widehat {ACB} = {30^ \circ }\,\, \Rightarrow \,\,\widehat {ACD} = {180^ \circ } - {30^ \circ } = {150^ \circ }\end{array}\)
Ta có: \(\overrightarrow {BC} .\overrightarrow {CA} = \overrightarrow {CD} .\overrightarrow {CA} = CD.CA.\cos \left( {\overrightarrow {CD} ,\overrightarrow {CA} } \right) = 2.2.\cos {150^ \circ } = - 3\)
Chọn D.
Bài 4.53 trang 68 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vectơ, thường là xác định mối quan hệ giữa các vectơ hoặc tính toán các đại lượng hình học dựa trên vectơ. Để giải bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 4.53. Tuy nhiên, dựa trên cấu trúc chung của sách bài tập Toán 10 Kết nối tri thức, bài tập này có thể thuộc một trong các dạng sau:
Ví dụ: Cho hình bình hành ABCD. Chứng minh rằng AB = DC và AD = BC.
Lời giải:
Ví dụ: Cho tam giác ABC, với AB = a, AC = b và góc BAC = 60°. Tính độ dài cạnh BC.
Lời giải:
Áp dụng định lý cosin trong tam giác ABC, ta có:
BC2 = AB2 + AC2 - 2.AB.AC.cos(BAC)
BC2 = a2 + b2 - 2.a.b.cos(60°)
BC2 = a2 + b2 - a.b
BC = √(a2 + b2 - a.b)
Ví dụ: Cho tam giác ABC. Chứng minh rằng AB + BC = AC.
Lời giải:
Đây là quy tắc cộng vectơ. AB + BC = AC theo quy tắc tam giác.
Bài 4.53 trang 68 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng trong hình học. Bằng cách nắm vững các kiến thức cơ bản và áp dụng các mẹo giải bài tập, học sinh có thể tự tin giải quyết bài toán này một cách hiệu quả.