Bài 8.34 trang 60 SBT Toán 10 Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học phẳng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.34 trang 60 SBT Toán 10 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hình sau đây được tạo thành từ hai họ đường thẳng vuông góc, mỗi họ gồm 6 đường thẳng song song.
Đề bài
Hình sau đây được tạo thành từ hai họ đường thẳng vuông góc, mỗi họ
gồm 6 đường thẳng song song.
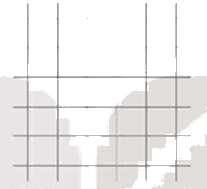
Hỏi có bao nhiêu hình chữ nhật khác nhau được tạo thành?
Phương pháp giải - Xem chi tiết
Áp dụng công thức tổ hợp và quy tắc nhân.
Lời giải chi tiết
Mỗi hình chữ nhật được tạo thành từ giao điểm của 2 đường thẳng của họ các đường đường thẳng nằm ngang và 2 đường thẳng của họ các đường thẳng nằm dọc.
Số cách chọn ra 2 đường thẳng từ 6 đường thẳng nằm ngang là: \(C_6^2 = 15\)cách
Số cách chọn ra 2 đường thẳng từ 6 đường thẳng nằm dọc là: \(C_6^2 = 15\) cách
Theo quy tắc nhân, số hình chữ nhật được tạo thành là: 15. 15= 225 cách
Bài 8.34 trang 60 SBT Toán 10 Kết nối tri thức yêu cầu chúng ta tìm hiểu về mối quan hệ giữa các vectơ và ứng dụng của chúng trong việc chứng minh các tính chất hình học. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi đi vào giải bài tập cụ thể, chúng ta cần phân tích đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài 8.34 thường yêu cầu chứng minh một đẳng thức vectơ hoặc một tính chất hình học nào đó. Việc phân tích đúng đề bài sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp.
Để giải bài 8.34 trang 60 SBT Toán 10 Kết nối tri thức, chúng ta sẽ thực hiện theo các bước sau:
Ví dụ, giả sử bài toán yêu cầu chứng minh rằng tứ giác ABCD là hình bình hành. Chúng ta có thể sử dụng tính chất của hình bình hành: hai vectơ đối diện bằng nhau. Cụ thể, chúng ta cần chứng minh rằng AB = DC và AD = BC.
Ngoài bài 8.34, SBT Toán 10 Kết nối tri thức còn có nhiều bài tập tương tự về vectơ. Các bài tập này thường yêu cầu:
Để giải các bài tập về vectơ một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Vectơ không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 8.34 trang 60 SBT Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng trong hình học. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng, xác định bởi điểm gốc và điểm cuối. |
| Tích vô hướng | Một phép toán giữa hai vectơ, cho ra một số thực. |
| Bảng tóm tắt các khái niệm quan trọng. | |