Bài 3.11 trang 39 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.11 trang 39, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng N80E với vận tốc 20 km/h.
Đề bài
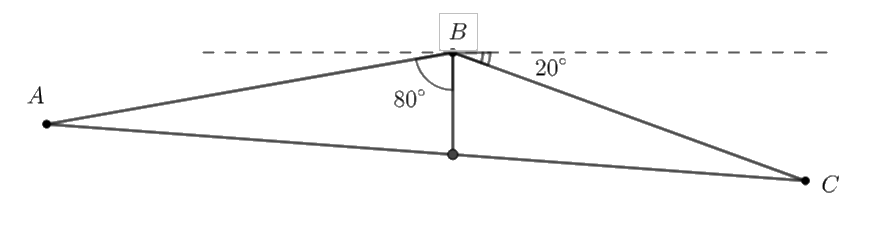
Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng \(N{80^ \circ }E\) với vận tốc 20 km/h. Sau khi đi được 30 phút, tàu chuyển sang hướng\(E{20^ \circ }S\) giữ nguyên vận tốc và chạy tiếp 36 phút nữa đến đảo Cát Bà. Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu ki lô mét.
Phương pháp giải - Xem chi tiết
- Đổi 30 phút = \(\frac{1}{2}\) giờ và 36 phút = \(\frac{3}{5}\) giờ
- Tính \(\widehat {ABC}\)
- Tính quãng đường \(AB,\,\,BC\)
- Áp dụng định lý côsin để tính quãng đường \(A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos ABC\)
Lời giải chi tiết
Xét \(\Delta ABC\) có \(\widehat B = {80^ \circ } + \left( {{{90}^ \circ } - {{20}^ \circ }} \right) = {150^ \circ }.\)
Độ dài quãng đường \(AB\) là: \(AB = 20.\frac{1}{2} = 10\,\,km.\)
Độ dài quãng đường \(BC\) là: \(BC = 20.\frac{3}{5} = 12\,\,km.\)
Khoảng cách từ điểm xuất phát A đến điểm đích C là:
Áp dụng định lý côsin, ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos ABC\\A{C^2} = {10^2} + {12^2} - 2.10.12.\cos {150^ \circ }\\A{C^2} = 100 + 144 - 240.\left( {\frac{{ - \sqrt 3 }}{2}} \right) \approx 452.\\ \Rightarrow \,\,AC \approx \sqrt {452} \approx 21\,\,km.\end{array}\)
Bài 3.11 trang 39 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh sử dụng kiến thức về vectơ để chứng minh các đẳng thức vectơ liên quan đến trung điểm, trọng tâm của tam giác. Để giải bài tập này một cách hiệu quả, cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ và các tính chất của trung điểm, trọng tâm.
Trước khi bắt đầu giải bài tập, hãy đọc kỹ đề bài và xác định rõ yêu cầu. Trong bài 3.11, chúng ta thường gặp các yêu cầu chứng minh đẳng thức vectơ liên quan đến các điểm đặc biệt trong tam giác. Các kiến thức cần thiết bao gồm:
Để giải bài 3.11, chúng ta sẽ sử dụng các kiến thức đã nêu trên. Dưới đây là một ví dụ về cách giải một dạng bài tập thường gặp:
Ví dụ: Cho tam giác ABC có M là trung điểm của BC. Chứng minh rằng AB + AC = 2AM.
Ta có: AM = AB + BM. Vì M là trung điểm của BC nên BM = MC. Do đó, BC = 2BM, suy ra BM = 1/2 BC.
Mặt khác, BC = AC - AB. Vậy BM = 1/2 (AC - AB).
Thay vào biểu thức AM = AB + BM, ta được: AM = AB + 1/2 (AC - AB) = AB + 1/2 AC - 1/2 AB = 1/2 AB + 1/2 AC = 1/2 (AB + AC).
Nhân cả hai vế với 2, ta được: 2AM = AB + AC.
Ngoài dạng bài tập chứng minh đẳng thức vectơ như trên, bài 3.11 còn có thể xuất hiện các dạng bài tập khác như:
Để giải các dạng bài tập này, cần vận dụng linh hoạt các kiến thức về vectơ, các phép toán vectơ và các tính chất của các điểm đặc biệt trong tam giác. Ngoài ra, việc vẽ hình chính xác và phân tích đề bài một cách kỹ lưỡng cũng rất quan trọng.
Để nắm vững kiến thức và kỹ năng giải bài tập về vectơ, các em học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp các em tự tin hơn trong quá trình học tập.
Bài 3.11 trang 39 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Hy vọng với hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.