Bài 2.18 trang 26 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.18 trang 26, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Miền nghiệm của hệ bất phương trình
Đề bài
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 1}\\{x + y \le 0}\\{y \ge 0}\end{array}} \right.\) là:
A. Một nửa mặt phẳng.
B. Miền tam giác.
C. Miền tứ giác.
D. Miền ngũ giác.
Phương pháp giải - Xem chi tiết
- Vẽ các bất phương trình trên cùng một mặt phẳng tọa độ \(Oxy.\)
- Xác định miền nghiệm của hệ bất phương trình đã cho.
Lời giải chi tiết
Miền nghiệm của bất phương trình \(x \ge - 1\) là nửa mặt phẳng bờ \(d:x = - 1\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(x + y \le 0\) là nửa mặt phẳng bờ \({d_1}:x + y = 0\) chứa điểm \(\left( { - 1;0} \right).\)
Miền nghiệm của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \({d_2}:y = 0\) chứa điểm \(\left( {0;1} \right).\)
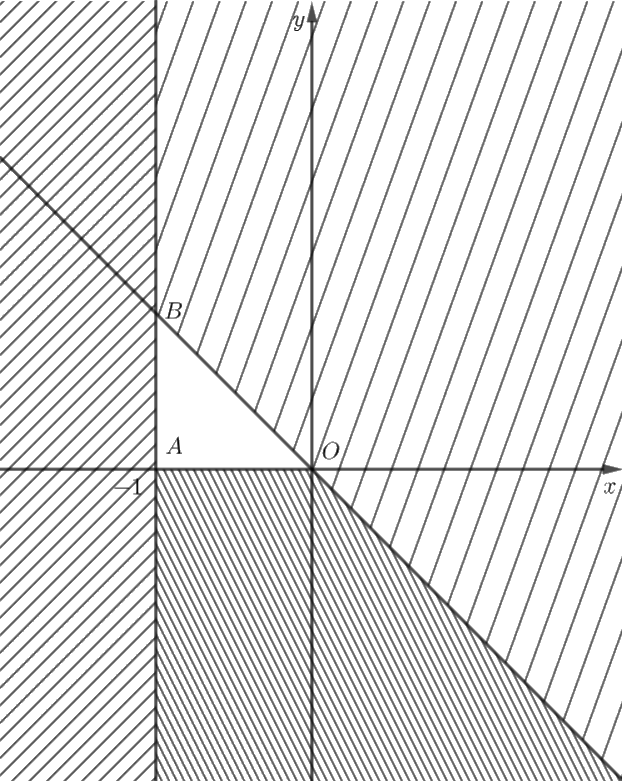
Miền nghiệm của hệ bất phương trình trên là tam giác \(OAB.\)
Chọn B
Bài 2.18 trang 26 sách bài tập Toán 10 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ, cụ thể là việc xác định mối quan hệ giữa các vectơ và sử dụng các phép toán vectơ để chứng minh một đẳng thức hoặc giải một bài toán hình học.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho tam giác ABC, gọi M là trung điểm của BC. Chứng minh rằng: $\overrightarrow{AM} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})$)
Để giải bài 2.18 trang 26, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bước 1: Phân tích bài toán
Đọc kỹ đề bài, xác định các vectơ đã cho và yêu cầu của bài toán. Trong bài toán này, chúng ta cần chứng minh một đẳng thức vectơ. Để chứng minh đẳng thức vectơ, chúng ta có thể sử dụng các phép biến đổi vectơ để đưa về hai vế của đẳng thức là tương đương.
Bước 2: Thực hiện chứng minh
(Phần này sẽ chứa lời giải chi tiết, bao gồm các bước biến đổi vectơ, sử dụng quy tắc hình bình hành, quy tắc tam giác, và các tính chất của phép toán vectơ. Ví dụ:)
Ta có: $\overrightarrow{AM} = \overrightarrow{AC} + \overrightarrow{CM}$. Vì M là trung điểm của BC nên $\overrightarrow{CM} = \frac{1}{2}\overrightarrow{CB}$. Do đó, $\overrightarrow{AM} = \overrightarrow{AC} + \frac{1}{2}\overrightarrow{CB}$.
Mặt khác, $\overrightarrow{CB} = \overrightarrow{AB} - \overrightarrow{AC}$. Thay vào biểu thức trên, ta được: $\overrightarrow{AM} = \overrightarrow{AC} + \frac{1}{2}(\overrightarrow{AB} - \overrightarrow{AC}) = \overrightarrow{AC} + \frac{1}{2}\overrightarrow{AB} - \frac{1}{2}\overrightarrow{AC} = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})$.
Vậy, $\overrightarrow{AM} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})$.
Bước 3: Kiểm tra lại kết quả
Kiểm tra lại các bước biến đổi vectơ để đảm bảo tính chính xác. Đảm bảo rằng các quy tắc và tính chất đã được áp dụng đúng cách.
Để củng cố kiến thức về vectơ và các phép toán vectơ, bạn có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về vectơ, bạn cần lưu ý những điều sau:
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 2.18 trang 26 sách bài tập Toán 10 Kết nối tri thức và tự tin hơn trong việc học tập môn Toán.
Bài 2.18 trang 26 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ. Việc nắm vững các kiến thức cơ bản về vectơ và các phép toán vectơ là điều cần thiết để giải quyết bài toán này một cách hiệu quả. Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán.