Bài 9.12 trang 66 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.12 trang 66, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trên một phố có hai quán ăn A, B. Bốn bạn Sơn, Hải, Văn, Đạo mỗi người chọn ngẫu nhiên một quán ăn. a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu. b) Tính xác suất để:
Đề bài
Trên một phố có hai quán ăn A, B. Bốn bạn Sơn, Hải, Văn, Đạo mỗi người chọn ngẫu nhiên một quán ăn.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất để:
• Tất cả đều vào một quán;
• Mỗi quán có đúng 2 bạn vào;
• Quán A có 3 bạn vào, quán B có 1 bạn vào
• Một quán có 3 bạn vào, quán kia có 1 bạn vào.
Phương pháp giải - Xem chi tiết
Sử dụng công thức xác suất cổ điển \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết
a) Sơ đồ cây
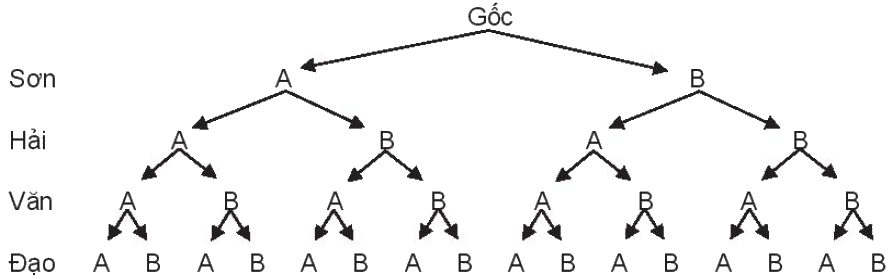
b) Ta có \(\Omega = \left\{ \begin{array}{l}AAAA;AAAB;AABA;AABB;ABAA;ABAB;ABBA;ABBB;\\BAAA;BAAB;BABA;BABB;BBAA;BBAB;BBBA;BBBB\end{array} \right\}\) .
Suy ra \(n\left( \Omega \right) = 16\).
+ Gọi \(E\) là biến cố \(E\): “Tất cả đều vào một quán”. \(E = \left\{ {AAAA,BBBB} \right\}\). Suy ra \(n\left( E \right) = 2 \Rightarrow P\left( E \right) = \frac{2}{{16}} = \frac{1}{8}\).
+ Gọi \(F\) là biến cố \(F\): “Mỗi quán có đúng hai bạn vào”. \(F = \left\{ {AABB,ABAB,ABBA,BAAB,BABA,BBAA} \right\}\). Suy ra \(n\left( F \right) = 6 \Rightarrow P\left( F \right) = \frac{6}{{16}} = \frac{3}{8}\).
+ Gọi \(G\) là biến cố \(G\): “Quán A có ba bạn vào, quán B có một bạn vào”.
\(G = \left\{ {AAAB;AABA;ABAA;BAAA} \right\}\). Suy ra \(n\left( G \right) = 4 \Rightarrow P\left( G \right) = \frac{4}{{16}} = \frac{1}{4}\).
+ Gọi K là biến cố K: “Một quán có ba bạn vào, quán kia có một bạn vào”.
Khi đó \(P\left( K \right) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\).
Bài 9.12 trang 66 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh sử dụng kiến thức về tích vô hướng của hai vectơ để chứng minh một số tính chất hình học. Để giải bài tập này, chúng ta cần nắm vững định nghĩa tích vô hướng, các công thức tính tích vô hướng và các ứng dụng của tích vô hướng trong việc xác định góc giữa hai vectơ, độ dài vectơ và tính chất vuông góc của hai vectơ.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 9.12, đề bài thường yêu cầu chúng ta chứng minh một đẳng thức vectơ hoặc một tính chất hình học nào đó. Để làm được điều này, chúng ta cần sử dụng các kiến thức đã học để biến đổi các biểu thức vectơ và chứng minh các mối quan hệ giữa các vectơ.
Để giải bài 9.12 trang 66, chúng ta sẽ thực hiện các bước sau:
Giả sử đề bài yêu cầu chứng minh rằng nếu AB vuông góc với CD thì AB.CD = 0. Chúng ta có thể giải bài toán này như sau:
Khi giải bài tập về tích vô hướng, chúng ta cần lưu ý một số điều sau:
Để củng cố kiến thức về tích vô hướng, các em có thể làm thêm một số bài tập tương tự như:
Bài 9.12 trang 66 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Hy vọng với hướng dẫn chi tiết trên, các em học sinh có thể tự tin giải bài tập này và đạt kết quả tốt trong môn Toán 10.