Bài 4.30 trang 65 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.30 trang 65, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
a) Chứng minh rằng các đường thẳng AC và BM vuông góc với nhau.
Đề bài
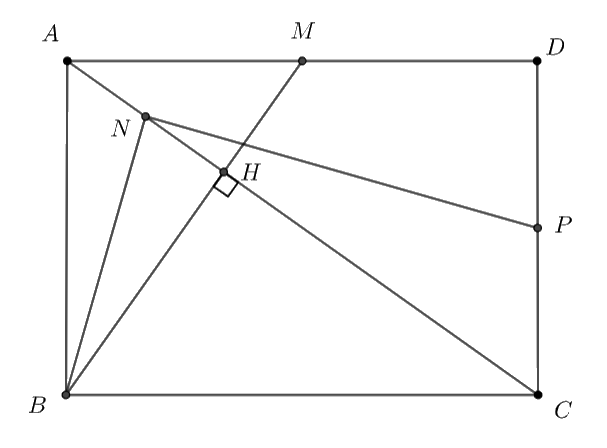
Cho hình chữ nhật \(ABCD\) có \(AB = 1,\,\,BC = \sqrt 2 .\) Gọi \(M\) là trung điểm của \(AD.\)
a) Chứng minh rằng các đường thẳng \(AC\) và \(BM\) vuông góc với nhau.
b) Gọi \(H\) là giao điểm của \(AC,\,\,BM.\) Gọi \(N\) là trung điểm của \(AH\) và \(P\) là trung điểm của \(CD.\) Chứng minh rằng tam giác \(NBP\) là một tam giác vuông.
Phương pháp giải - Xem chi tiết
- Tính các vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BM} \) xong tính tích vô hướng của hai vectơ \(\overrightarrow {AC} .\overrightarrow {BM} \)
- Tính độ dài các cạnh \(AC,\,\,AH\)
- Tính các vectơ \(\overrightarrow {NB} \) và \(\overrightarrow {NP} \) xong tính tích vô hướng của hai vectơ \(\overrightarrow {NB} .\overrightarrow {NP} \)
Lời giải chi tiết
a) Ta có: \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \) (quy tắc hình bình hành)
Ta có: \(\overrightarrow {BM} = \overrightarrow {AM} - \overrightarrow {AB} = \frac{1}{2}\overrightarrow {AD} - \overrightarrow {AB} \)
\( \Rightarrow \) \(\overrightarrow {AC} .\overrightarrow {BM} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\left( {\frac{1}{2}\overrightarrow {AD} - \overrightarrow {AB} } \right)\)
\(\begin{array}{l} = \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AD} - {\overrightarrow {AB} ^2} + \frac{1}{2}{\overrightarrow {AD} ^2} - \overrightarrow {AB} .\overrightarrow {AD} \\ = - {\overrightarrow {AB} ^2} + \frac{1}{2}{\overrightarrow {AD} ^2} = - 1 + \frac{1}{2}\left( {\sqrt 2 } \right) - 1 + 1 = 0\end{array}\)
\( \Rightarrow \) \(\overrightarrow {AC} \bot \overrightarrow {BM} \) \( \Rightarrow \) \(AC \bot BM\)
b) Xét \(\Delta ABC\) vuông tại \(B\) có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {1 + {{\left( {\sqrt 2 } \right)}^2}} = \sqrt 3 \) (1)
Xét \(\Delta ABN\) vuông tại \(A\) có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{M^2}}}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow \,\,\frac{1}{{A{H^2}}} = \frac{1}{{{1^2}}} + \frac{1}{{{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}}} = 1 + 2 = 3\)
\( \Rightarrow \,\,AH = \frac{{\sqrt 3 }}{3}\) (2)
Từ (1) và (2) \( \Rightarrow \) \(AH = \frac{1}{3}AC\)
Ta có: \(\overrightarrow {NB} = \overrightarrow {AB} - \overrightarrow {AN} = \overrightarrow {AB} - \frac{1}{2}\overrightarrow {AH} = \overrightarrow {AB} - \frac{1}{6}\overrightarrow {AC} = \frac{5}{6}\overrightarrow {AB} - \frac{1}{6}\overrightarrow {AD} \)
Ta có: \(\overrightarrow {NP} = \overrightarrow {CP} - \overrightarrow {CN} = \frac{1}{2}\overrightarrow {CD} - \frac{5}{6}\overrightarrow {CA} = \frac{5}{6}\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} = \frac{5}{6}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AB} \)
\( \Rightarrow \) \(\overrightarrow {NB} .\overrightarrow {NP} = \left( {\frac{5}{6}\overrightarrow {AB} - \frac{1}{6}\overrightarrow {AD} } \right)\left( {\frac{5}{6}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AB} } \right)\)
\(\begin{array}{l} = \frac{{25}}{{36}}\overrightarrow {AB} .\overrightarrow {AD} + \frac{5}{{18}}{\overrightarrow {AB} ^2} - \frac{5}{{36}}{\overrightarrow {AD} ^2} - \frac{1}{{18}}\overrightarrow {AB} .\overrightarrow {AD} \\ = \frac{5}{{18}}{\overrightarrow {AB} ^2} - \frac{5}{{36}}{\overrightarrow {AD} ^2} = \frac{5}{{18}}.1 - \frac{5}{{36}}.\left( {\sqrt 2 } \right) = \frac{5}{{18}} - \frac{5}{{18}} = 0\end{array}\)
\( \Rightarrow \) \(\overrightarrow {NB} \bot \overrightarrow {NP} \) \( \Rightarrow \) \(NB \bot NP\)
\( \Rightarrow \) \(\Delta NBP\) vuông tại \(N\).
Bài 4.30 trang 65 sách bài tập Toán 10 Kết nối tri thức thường xoay quanh việc sử dụng các tính chất của vectơ, đặc biệt là các phép toán cộng, trừ vectơ, tích của một số với một vectơ, và các ứng dụng của vectơ trong việc chứng minh các tính chất hình học.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức cơ bản:
Để giải bài 4.30 trang 65 hiệu quả, cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ cung cấp một hình vẽ hoặc một mô tả về các điểm, đường thẳng, và yêu cầu chứng minh một mối quan hệ nào đó giữa chúng bằng cách sử dụng vectơ.
(Ở đây sẽ là lời giải chi tiết của bài toán 4.30, bao gồm các bước giải, giải thích rõ ràng, và sử dụng các ký hiệu toán học chính xác. Ví dụ, nếu bài toán yêu cầu chứng minh hai đường thẳng song song, lời giải sẽ trình bày cách sử dụng vectơ chỉ phương để chứng minh hai vectơ chỉ phương của hai đường thẳng cùng phương.)
Ví dụ (giả định):
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2
Vì M là trung điểm của BC, ta có: overrightarrow{BM} =overrightarrow{MC}.
Suy ra: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM} =overrightarrow{AB} +overrightarrow{MC} =overrightarrow{AB} + (overrightarrow{AC} -overrightarrow{AM}).
Do đó: 2overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC}.
Vậy: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 (đpcm).
Các bài tập tương tự bài 4.30 thường yêu cầu:
Để giải các bài tập này, cần nắm vững các kiến thức cơ bản về vectơ, áp dụng các quy tắc và tính chất một cách linh hoạt, và kết hợp với các kiến thức hình học đã học.
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, các em học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Bài 4.30 trang 65 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên đây, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.