Chào mừng các em học sinh đến với bài giải bài 6.10 trang 9 sách bài tập Toán 10 - Kết nối tri thức. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giaitoan.edu.vn là địa chỉ học toán online uy tín, cung cấp đầy đủ các bài giải sách bài tập Toán 10, Toán 11, Toán 12 và các kiến thức toán học khác.
Có hai địa điểm A, B cùng nằm trên một tuyến quốc lộ thẳng. Khoảng cách giữa A và B là 20 km. Một xe máy xuất phát từ A lúc 6 giờ và chạy với vận tốc 40 km/h theo chiều từ A đến B.
Đề bài
Có hai địa điểm A, B cùng nằm trên một tuyến quốc lộ thẳng. Khoảng cách giữa A và B là 20 km. Một xe máy xuất phát từ A lúc 6 giờ và chạy với vận tốc 40 km/h theo chiều từ A đến B. Một ô tô xuất phát từ B lúc 8 giờ và chạy với vận tốc 80 km/h theo cùng chiều với xe máy. Coi chuyển động của xe máy và ô tô là thẳng đều. Chọn A làm mốc, chọn thời điểm 6 giờ làm mốc thời gian và chọn chiều từ A đến B làm chiều dương. Khi đó tọa độ của xe máy và ô tô sẽ là những hàm số của biến thời gian.
a) Viết PT chuyển động của xe máy và ô tô (tức là công thức hàm tọa độ theo thời gian)
b) Vẽ đồ thị hàm tọa độ của xe máy và ô tô trên cùng một hệ trục tọa độ
c) Căn cứ vào đồ thị vẽ được, hãy xác định vị trí và thời điểm ô tô đuổi kịp xe máy
d) Kiểm tra lại kết quả tìm được ở câu c) bằng cách giải các phương trình chuyển động của xe máy và ô tô.
Phương pháp giải - Xem chi tiết
Bước 1: Gọi t là thời gian chuyển động của xe máy. Biểu diễn quãng đường đi được của xe máy (S1) và ô tô (S2) theo t (là PT chuyển động của xe máy và ô tô)
Bước 2: Vẽ đồ thị hàm số S1 và S2 theo biến t
Bước 3: Tìm tọa độ giao điểm của 2 đồ thị (vị trí ô tô đuổi kịp xe máy) bằng hình vẽ và lập luận
Lời giải chi tiết
a) Gọi t (t > 0) là thời gian chuyển động của xe máy
Quãng đường xe máy đi được là: S1 = 40t (km)
Quãng đường ô tô đi được là: S2 = AB + 80(t – 2) = 80t – 140 (km)
\( \Rightarrow \) Phương trình chuyển động của xe máy là: \(y = {S_1}(t) = 40t\), của ô tô là: \(y = {S_2}(t) = 80t - 140\)
b) Ta có đồ thị
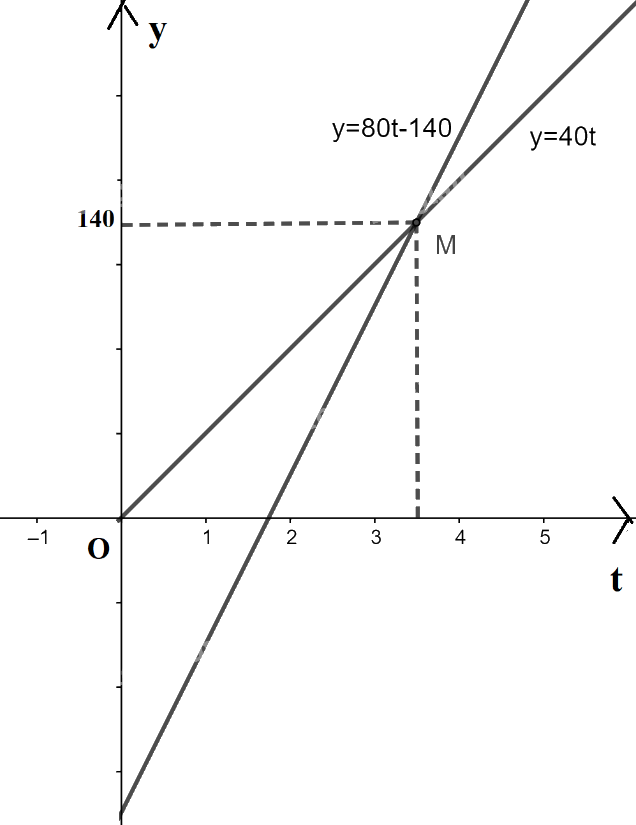
c) Từ đồ thị ta thấy 2 đồ thị cắt nhau tại điểm \(M\left( {\frac{7}{2};140} \right)\). Như vậy ô tô đuổi kịp xe máy lúc 9h 30 phút tại vị trí cách A 140 km
d) Xét PT hoành độ: \(40t = 80t - 140 \Leftrightarrow t = \frac{7}{2}\)
Với \(t = \frac{7}{2}\) thì y = 140. Vậy ô tô đuổi kịp xe máy lúc 9h 30 phút tại vị trí cách A 140 km
Bài 6.10 trang 9 sách bài tập Toán 10 - Kết nối tri thức yêu cầu chúng ta vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết bài toán cụ thể. Bài toán này thường liên quan đến việc chứng minh đẳng thức vectơ, tìm tọa độ của vectơ, hoặc xác định mối quan hệ giữa các vectơ trong một hình học nhất định.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Đồng thời, cần ôn lại các kiến thức liên quan như:
(Nội dung lời giải chi tiết bài 6.10 trang 9 sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và minh họa bằng hình vẽ nếu cần thiết. Lời giải sẽ được chia thành các bước nhỏ để dễ theo dõi và hiểu.)
Ví dụ, nếu bài toán yêu cầu chứng minh một đẳng thức vectơ, chúng ta có thể sử dụng các quy tắc biến đổi vectơ để đưa về dạng đơn giản hơn. Nếu bài toán yêu cầu tìm tọa độ của vectơ, chúng ta có thể sử dụng công thức tính tọa độ của vectơ dựa trên tọa độ của các điểm.
Ngoài bài 6.10, còn rất nhiều bài tập tương tự trong sách bài tập Toán 10 - Kết nối tri thức. Để giải quyết các bài tập này, chúng ta có thể áp dụng các phương pháp sau:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 6.10 trang 9 sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng giúp các em hiểu sâu hơn về vectơ và các phép toán vectơ. Hy vọng với lời giải chi tiết và các phương pháp giải đã trình bày, các em sẽ tự tin giải quyết bài toán này và các bài tập tương tự.
Lưu ý:
Vectơ có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học kỹ thuật, ví dụ như:
Việc nắm vững kiến thức về vectơ sẽ giúp các em hiểu sâu hơn về các ứng dụng này và có thể giải quyết các bài toán thực tế một cách hiệu quả.
Chúc các em học tập tốt!