Bài 4.15 trang 54 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập này.
Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O.
Đề bài
Cho tam giác \(ABC\) có trực tâm \(H,\) trọng tâm \(G\) và tâm đường tròn ngoại tiếp \(O.\)
a) Gọi \(M\) là trung điểm của \(BC.\) Chứng minh rằng \(\overrightarrow {AH} = 2\overrightarrow {OM} .\)
b) Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\)
c) Chứng minh rằng ba điểm \(G,\,\,H,\,\,O\) cùng thuộc một đường thẳng.
Phương pháp giải - Xem chi tiết
- Chứng minh tứ giác \(ABHC\) là hình bình hành
- Chứng minh \(MO\) là đường trung bình của \(\Delta AA'H\)
- Chứng minh \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OM} \) từ đó rút ra kết luận \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\)
- Chứng minh \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} .\)
- Chứng minh \(\overrightarrow {OH} \) và \(\overrightarrow {OG} \) cùng phương
Lời giải chi tiết
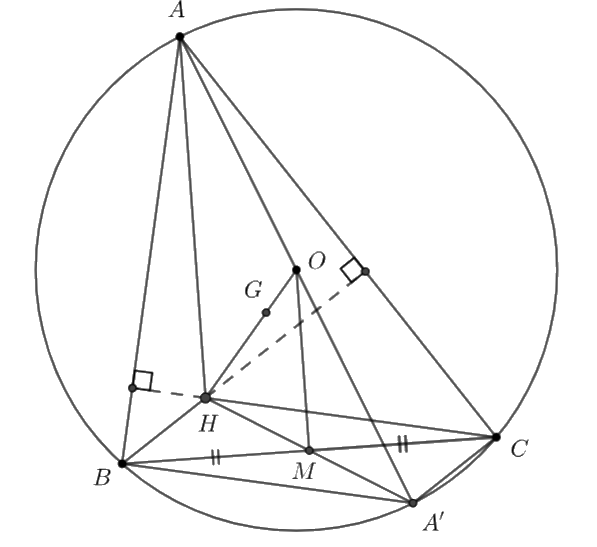
a) Xét \((O)\) có: \(\widehat {ABA'} = \widehat {ACA'} = {90^ \circ }\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow A'C \bot AC\) và \(A'B \bot AB\) (1)
Ta có: \(H\) là trực tâm của tam giác \(ABC.\)
\( \Rightarrow BH \bot AC\) và \(CH \bot AB\) (2)
Từ (1) và (2) \( \Rightarrow \) \(BH\)//\(A'C\) và \(A'B\)//\(CH.\)
Xét tứ giác \(ABHC\) có: \(BH\)//\(A'C\) và \(A'B\)//\(CH\)
\( \Rightarrow \) tứ giác \(ABHC\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \overrightarrow {BH} = \overrightarrow {A'C} \)
Ta có: tứ giác \(ABHC\) là hình bình hành
nên \(M\) là trung điểm của \(A'H\)
Xét \(\Delta AA'H\) có: \(M\) là trung điểm của \(A'H\)
\(O\) là trung điểm của \(AA'\)
\( \Rightarrow \) \(MO\) là đường trung bình của \(\Delta AA'H\)
\( \Rightarrow \) \(MO\)//\(AH\) và \(2MO = AH\)
\( \Rightarrow \) hai vectơ \(\overrightarrow {MO} ,\,\,\overrightarrow {AH} \) cùng hướng và \(2\overrightarrow {OM} = \overrightarrow {AH} .\)
b) Ta có:
\(\overrightarrow {OB} + \overrightarrow {OC} = \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MC} } \right) = 2\overrightarrow {OM} + \left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = 2\overrightarrow {OM} \)
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OA} + 2\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {AH} = \overrightarrow {OH} \) (3)
c) Ta có: \(G\) là trọng tâm của \(\Delta ABC\)
nên \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} .\) (4)
Từ (3) và (4) \( \Rightarrow \overrightarrow {OH} = 3\overrightarrow {OG} \)
\( \Rightarrow \overrightarrow {OH} \) và \(\overrightarrow {OG} \) cùng phương
hay ba điểm \(G,\,\,H,\,\,O\) cùng thuộc một đường thẳng.
Bài 4.15 trang 54 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ về vectơ, các phép toán vectơ và cách áp dụng chúng vào giải quyết vấn đề. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo hai vectơ AB và AC.
Để tìm vectơ AM theo hai vectơ AB và AC, ta sử dụng quy tắc trung điểm và các phép toán vectơ.
Kết quả này cho thấy vectơ AM là trung bình cộng của hai vectơ AB và AC. Điều này hoàn toàn phù hợp với quy tắc trung điểm và tính chất của vectơ.
Giả sử A(0;0), B(2;0), C(0;2). Khi đó, M là trung điểm của BC, có tọa độ M(1;1). Ta có:
Ta thấy vectơ AM = (AB + AC) / 2 = ((2;0) + (0;2)) / 2 = (1;1), điều này chứng minh kết quả trên là đúng.
Bài toán này có thể được mở rộng để giải quyết các bài toán liên quan đến trọng tâm của tam giác, đường trung tuyến và các tính chất của vectơ trong hình học.
Khi giải các bài toán về vectơ, cần chú ý đến quy tắc cộng, trừ vectơ, quy tắc trung điểm và các tính chất của vectơ để đảm bảo tính chính xác của kết quả.
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự trong sách bài tập Toán 10 - Kết nối tri thức với cuộc sống. Hãy nhớ áp dụng các kiến thức và kỹ năng đã học để giải quyết các bài toán một cách hiệu quả.
Bài 4.15 trang 54 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh hiểu rõ hơn về vectơ và các ứng dụng của chúng trong hình học. Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập này một cách dễ dàng và hiệu quả.