Bài 2.1 trang 18 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh phải nắm vững định nghĩa, tính chất của tập hợp và cách thực hiện các phép toán hợp, giao, hiệu, bù của hai tập hợp.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.1 trang 18 sách bài tập Toán 10 Kết nối tri thức, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cho bất phương trình bậc nhất hai ẩn - 3x + y < 4. a) Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng tọa độ.
Đề bài
Cho bất phương trình bậc nhất hai ẩn \( - 3x + y < 4.\)
a) Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng tọa độ.
b) Từ đó suy ra miền nghiệm của bất phương trình \( - 3x + y \le 4\) và miền nghiệm của bất phương trình \( - 3x + y \ge 4.\)
Phương pháp giải - Xem chi tiết
- Vẽ đường thẳng \(d: - 3x + y = 4\) trên mặt phẳng tọa độ \(Oxy.\)
- Xác định miền nghiệm của bất phương trình đã cho
- Tìm miền nghiệm của bất phương trình \( - 3x + y \le 4\) và \( - 3x + y \ge 4.\)
Lời giải chi tiết
a) Ta biểu diễn miền nghiệm của bất phương trình như sau:
Vẽ đường thẳng \(d: - 3x + y = 4\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn điểm \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \(d\) và thay vào biểu thức \( - 3x + y,\) ta được \( - 3.0 + 0 = 0 < 4.\)
Do đó, miền nghiệm của bất phương trình đã cho là nửa mặt phẳng bờ \(d\) chứa gốc tọa độ mà (không kể \(d\)) (miền không bị gạch).
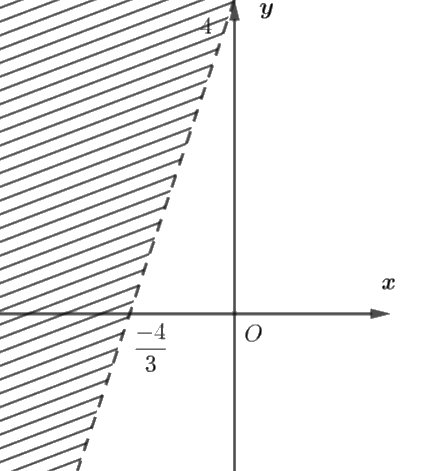
b) Miền nghiệm của phương trình \( - 3x + y \le 4\) chính là nửa mặt phẳng \(d\) chứa gốc tọa độ.
Miền nghiệm của phương trình \( - 3x + y \ge 4\)chính là nửa mặt phẳng \(d\) không chứa gốc tọa độ (miền bị gạch).
Bài 2.1 trang 18 sách bài tập Toán 10 Kết nối tri thức yêu cầu chúng ta thực hiện các phép toán trên tập hợp. Để giải bài này một cách hiệu quả, trước hết cần nắm vững các khái niệm cơ bản về tập hợp.
1. Tập hợp là gì? Tập hợp là một khái niệm cơ bản trong toán học, dùng để chứa các đối tượng được xác định rõ ràng. Các đối tượng này được gọi là các phần tử của tập hợp.
2. Cách biểu diễn tập hợp: Tập hợp thường được biểu diễn bằng cách liệt kê các phần tử trong dấu ngoặc nhọn {}, hoặc bằng cách chỉ ra tính chất đặc trưng của các phần tử.
3. Các phép toán trên tập hợp:
Để giải bài 2.1 trang 18, chúng ta cần áp dụng các định nghĩa và tính chất của các phép toán trên tập hợp đã nêu ở trên. Dưới đây là hướng dẫn chi tiết:
Bài 2.1: Cho hai tập hợp A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Hãy tìm:
Lời giải:
1. A ∪ B: A ∪ B = {1, 2, 3, 4, 5, 6} (Tập hợp chứa tất cả các phần tử thuộc A hoặc B)
2. A ∩ B: A ∩ B = {3, 4} (Tập hợp chứa tất cả các phần tử thuộc cả A và B)
3. A \ B: A \ B = {1, 2} (Tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B)
4. B \ A: B \ A = {5, 6} (Tập hợp chứa tất cả các phần tử thuộc B nhưng không thuộc A)
Để củng cố kiến thức về các phép toán trên tập hợp, bạn có thể tự giải thêm các bài tập sau:
Khi giải các bài tập về tập hợp, cần chú ý:
Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ hiểu rõ hơn về cách giải bài 2.1 trang 18 sách bài tập Toán 10 Kết nối tri thức và tự tin hơn trong việc học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các bạn trên con đường chinh phục kiến thức Toán học!