Bài 1.6 trang 8 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc nhất một ẩn. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm ra nghiệm của phương trình.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.6 trang 8 sách bài tập Toán 9 - Kết nối tri thức tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho các cặp số (-2; 2), (1; 1), (4; 1), (8; -2) và hai phương trình: (x + 3y = 4); (1) (2x - 5y = - 3). (2) a) Những cặp số nào là nghiệm của phương trình (1)? b) Cặp số nào là nghiệm của hệ gồm hai phương trình (1) và phương trình (2)? c) Vẽ hai đường thẳng (d:x + 3y = 4) và (d':2x - 5y = - 3) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Đề bài
Cho các cặp số (-2; 2), (1; 1), (4; 1), (8; -2) và hai phương trình:
\(x + 3y = 4\); (1)
\(2x - 5y = - 3\). (2)
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ gồm hai phương trình (1) và phương trình (2)?
c) Vẽ hai đường thẳng \(d:x + 3y = 4\) và \(d':2x - 5y = - 3\) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Phương pháp giải - Xem chi tiết
a) Nếu tại \(x = {x_0}\) và \(y = {y_0}\) ta có \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là nghiệm của phương trình bậc nhất hai ẩn \(ax + by = c\).
b) Mỗi cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của hệ \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).
Lời giải chi tiết
a) Với \(x = - 2,y = 2\) ta có: \( - 2 + 3.2 = 4\) nên (-2; 2) là nghiệm của phương trình \(x + 3y = 4\).
Với \(x = 1,y = 1\) ta có: \(1 + 3.1 = 4\) nên (1; 1) là nghiệm của phương trình \(x + 3y = 4\).
Với \(x = 4,y = 1\) ta có: \(4 + 3.1 = 7 \ne 4\) nên (4; 1) không là nghiệm của phương trình \(x + 3y = 4\).
Với \(x = 8,y = - 2\) ta có: \(8 + 3.\left( { - 2} \right) = 2 \ne 4\) nên (8; -2) là nghiệm của phương trình \(x + 3y = 4\).
Vậy cặp số là nghiệm của phương trình (1) là (-2; 2), (1; 1).
b) Với \(x = 1,y = 1\) ta có: \(2.1 - 5.1 = - 3\) nên (1; 1) là nghiệm của phương trình \(2x - 5y = - 3\).
Vậy cặp số (1; 1) là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2).
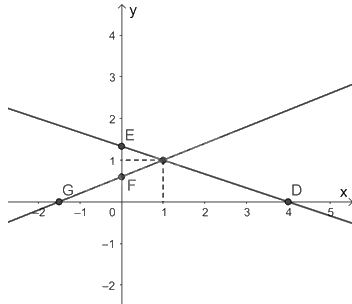
c) Đường thẳng \(x + 3y = 4\) đi qua hai điểm \(E\left( {0;\frac{4}{3}} \right)\) và \(D\left( {4;0} \right)\).
Đường thẳng \(2x - 5y = - 3\) đi qua hai điểm \(F\left( {0;\frac{3}{5}} \right)\) và \(G\left( {\frac{{ - 3}}{2};0} \right)\).
Do đó, đồ thị hàm số của hai đường thẳng \(x + 3y = 4\) và \(2x - 5y = - 3\) trên cùng một mặt phẳng tọa độ là:
Bài 1.6 trang 8 sách bài tập Toán 9 - Kết nối tri thức tập 1 thuộc chương 1: Phương trình bậc nhất một ẩn. Bài tập này tập trung vào việc giải phương trình bậc nhất một ẩn, một kiến thức nền tảng trong chương trình Toán 9.
Bài tập yêu cầu giải các phương trình sau:
Để giải phương trình bậc nhất một ẩn, ta thực hiện các bước sau:
2(x + 1) - 3 = 5
2x + 2 - 3 = 5
2x - 1 = 5
2x = 6
x = 3
3x - 2(x - 1) = 7
3x - 2x + 2 = 7
x + 2 = 7
x = 5
5(x - 2) + 3(x + 1) = 10
5x - 10 + 3x + 3 = 10
8x - 7 = 10
8x = 17
x = 17/8
4x + 2 = 3x - 1
4x - 3x = -1 - 2
x = -3
x - 5 = 2x + 3
x - 2x = 3 + 5
-x = 8
x = -8
Phương trình bậc nhất một ẩn có nhiều ứng dụng trong thực tế, ví dụ như:
Để rèn luyện thêm kỹ năng giải phương trình bậc nhất một ẩn, các em có thể làm thêm các bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 1.
Bài 1.6 trang 8 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh nắm vững kiến thức về phương trình bậc nhất một ẩn. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi làm bài tập.