Bài 8.12 trang 47 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.12 trang 47, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Có ba chiếc hộp. Hộp A chứa 2 tấm thẻ ghi các số 1, 2. Hộp B chứa 3 tấm thẻ ghi các số 1, 2, 3. Hộp C chứa 4 quả cầu ghi các số 1, 2, 3, 4. Bạn Lan rút ngẫu nhiên đồng thời một tấm thẻ từ mỗi hộp A và B. Bạn Linh lấy ngẫu nhiên một quả cầu từ hộp C. Tính xác suất của các biến cố sau: a) E: “Ba số ghi trên hai tấm thẻ và quả cầu là khác nhau”; b) F: “Tổng ba số ghi trên hai tấm thẻ và quả cầu bằng 5”.
Đề bài
Có ba chiếc hộp. Hộp A chứa 2 tấm thẻ ghi các số 1, 2. Hộp B chứa 3 tấm thẻ ghi các số 1, 2, 3. Hộp C chứa 4 quả cầu ghi các số 1, 2, 3, 4. Bạn Lan rút ngẫu nhiên đồng thời một tấm thẻ từ mỗi hộp A và B. Bạn Linh lấy ngẫu nhiên một quả cầu từ hộp C. Tính xác suất của các biến cố sau:
a) E: “Ba số ghi trên hai tấm thẻ và quả cầu là khác nhau”;
b) F: “Tổng ba số ghi trên hai tấm thẻ và quả cầu bằng 5”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Kết quả có thể khi bạn Lan rút ngẫu nhiên một tấm thẻ từ mỗi hộp A và B:
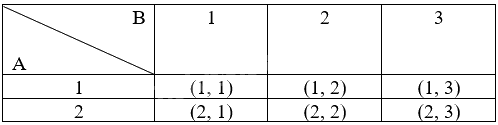
Kết quả có thể của phép thử:
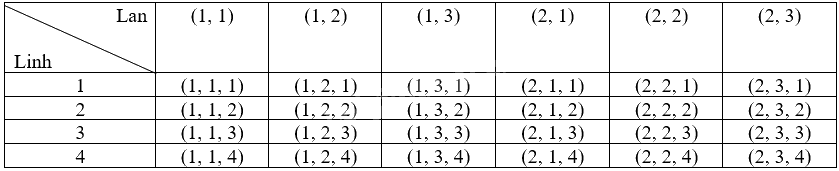
Có 24 kết quả có thể đồng là khả năng nên số phần tử của không gian mẫu là 24.
a) Có 8 kết quả thuận lợi cho biến cố E là:
(2, 3, 1), (1, 3, 2), (1, 2, 3), (2, 1, 3), (1, 2, 4), (1, 3, 4), (2, 1, 4), (2, 3, 4).
Vậy\(P\left( E \right) = \frac{8}{{24}} = \frac{1}{3}\).
b) Có 5 kết quả thuận lợi cho biến cố F là:
(1, 1, 3), (1, 2, 2), (1, 3, 1), (2, 1, 2), (2, 2, 1).
Vậy \(P\left( F \right) = \frac{5}{{24}}\).
Bài 8.12 trang 47 sách bài tập Toán 9 - Kết nối tri thức tập 2 thuộc chương Hàm số bậc nhất và hàm số bậc hai. Bài toán này thường yêu cầu học sinh xác định hệ số góc, điểm đi qua của đường thẳng, hoặc tìm giao điểm của hai đường thẳng.
Trước khi bắt đầu giải bài, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Xác định các thông tin đã cho và những gì cần tìm. Ví dụ, đề bài có thể yêu cầu tìm phương trình đường thẳng đi qua hai điểm, hoặc tìm giao điểm của đường thẳng và parabol.
Để giải bài 8.12 trang 47, học sinh cần nắm vững các kiến thức sau:
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng và kết quả cuối cùng. Ví dụ:)
Giả sử đề bài yêu cầu tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(-1; 0). Ta thực hiện như sau:
Ngoài bài 8.12, còn rất nhiều bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức về hàm số bậc nhất và bậc hai, cũng như các phương pháp giải hệ phương trình và phương trình bậc hai.
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp học sinh tự tin hơn khi làm bài kiểm tra và thi cử.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong sách giáo khoa và sách bài tập Toán 9 - Kết nối tri thức tập 2. Chúng tôi hy vọng rằng, với sự hỗ trợ của Giaitoan.edu.vn, các em học sinh sẽ học Toán 9 một cách hiệu quả và đạt kết quả cao.
Tìm phương trình đường thẳng đi qua điểm M(2; -1) và có hệ số góc bằng -2.
(Lời giải: Áp dụng công thức y = ax + b, thay a = -2 và điểm M(2; -1) vào, ta tìm được b = 3. Vậy phương trình đường thẳng là y = -2x + 3)
Bài 8.12 trang 47 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và bậc hai. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.