Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 của giaitoan.edu.vn. Chúng tôi xin giới thiệu bộ giải đáp chi tiết các câu hỏi trắc nghiệm trang 17, 18 sách bài tập Toán 9 - Kết nối tri thức tập 1, giúp các em ôn luyện và nắm vững kiến thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp lời giải chính xác, dễ hiểu, cùng với phương pháp giải bài tập hiệu quả nhất.
Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn? A. (left{ begin{array}{l}2x + y = 3x - z = - 1end{array} right.). B. (left{ begin{array}{l}2x + y = 3�x + 0y = 1end{array} right.). C. (left{ begin{array}{l}2x + y = 3�x - y = - 1end{array} right.). D. (left{ begin{array}{l}2x + y = 3x + {y^2} = 1end{array} right.).
Trả lời câu hỏi Câu 3 trang 18 SBT Toán 9 Kết nối tri thức
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 2), N(2; 3), P(-1; -1), Q(5; 8). Đường thẳng \(3x - 2y = - 1\) đi qua hai điểm nào trong các điểm đã cho?
A. M và N.
B. M và P.
C. P và Q.
D. N và P.
Phương pháp giải:
Nếu tại \(x = {x_0}\) và \(y = {y_0}\) ta có: \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì đường thẳng \(ax + by = c\) đi qua điểm A\(\left( {{x_0};{y_0}} \right)\).
Lời giải chi tiết:
Với \(x = 1,y = 2\) ta có: \(3.1 - 2.2 = - 1\) nên điểm M(1; 2) thuộc đường thẳng \(3x - 2y = - 1\).
Với \(x = 2,y = 3\) ta có: \(3.2 - 2.3 = 0 \ne - 1\) nên điểm N(2; 3) không thuộc đường thẳng \(3x - 2y = - 1\).
Với \(x = - 1,y = - 1\) ta có: \(3.\left( { - 1} \right) - 2.\left( { - 1} \right) = - 1\) nên điểm P(-1; -1) thuộc đường thẳng \(3x - 2y = - 1\).
Với \(x = 5,y = 8\) ta có: \(3.5 - 2.8 = - 1\) nên điểm Q(5; 8) thuộc đường thẳng \(3x - 2y = - 1\).
Vậy đường thẳng \(3x - 2y = - 1\) đi qua các điểm M, P, Q.
Chọn B, C
Trả lời câu hỏi Câu 2 trang 17 SBT Toán 9 Kết nối tri thức
Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x + 3y = - 1\\2x - y = 7\end{array} \right.\) là
A. (-1; 1).
B. (3; -1).
C. \(\left( {\frac{1}{2}; - 1} \right)\).
D. (2; -3).
Phương pháp giải:
Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình.
Lời giải chi tiết:
Sử dụng máy tính cầm tay, ta có nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x + 3y = - 1\\2x - y = 7\end{array} \right.\) là (2; -3).
Chọn D
Trả lời câu hỏi Câu 1 trang 17 SBT Toán 9 Kết nối tri thức
Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn?
A. \(\left\{ \begin{array}{l}2x + y = 3\\x - z = - 1\end{array} \right.\).
B. \(\left\{ \begin{array}{l}2x + y = 3\\0x + 0y = 1\end{array} \right.\).
C. \(\left\{ \begin{array}{l}2x + y = 3\\0x - y = - 1\end{array} \right.\).
D. \(\left\{ \begin{array}{l}2x + y = 3\\x + {y^2} = 1\end{array} \right.\).
Phương pháp giải:
Một cặp gồm hai phương trình bậc nhất hai ẩn \(ax + by = c\) và \(a'x + b'y = c'\) được gọi là một hệ phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (*).
Lời giải chi tiết:
Hệ \(\left\{ \begin{array}{l}2x + y = 3\\0x - y = - 1\end{array} \right.\) là hệ hai phương trình bậc nhất hai ẩn.
Chọn C
Trả lời câu hỏi Câu 4 trang 18 SBT Toán 9 Kết nối tri thức
Giá trị của a và b để đường thẳng \(y = ax + b\) đi qua hai điểm (1; -1) và (-1; 5) là
A. \(a = 1,b = - 2\).
B. \(a = - 5,b = 1\).
C. \(a = - 3,b = 2\).
D. \(a = - 1,b = 0\).
Phương pháp giải:
+ Vì đường thẳng \(y = ax + b\) đi qua hai điểm (1; -1) và (-1; 5) nên: \(\left\{ \begin{array}{l}a + b = - 1\\ - a + b = 5\end{array} \right.\)
+ Giải hệ phương trình vừa tìm được bằng phương pháp cộng đại số ta tìm được a, b.
Lời giải chi tiết:
Vì đường thẳng \(y = ax + b\) đi qua hai điểm (1; -1) và (-1; 5) nên: \(\left\{ \begin{array}{l}a + b = - 1\\ - a + b = 5\end{array} \right.\)
Cộng từng vế của hai phương trình trong hệ ta được: \(2b = 4\), suy ra \(b = 2\). Thay \(b = 2\) vào phương trình thứ nhất của hệ ta được: \(a + 2 = - 1\), suy ra \(a = - 3\).
Chọn C
Trả lời câu hỏi Câu 5 trang 18 SBT Toán 9 Kết nối tri thức
Hệ phương trình nào sau đây có nghiệm duy nhất?
A. \(\left\{ \begin{array}{l}x - 2y = 3\\2x - 4y = 5\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x - 2y = 3\\ - 2x + 4y = - 6\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x - 2y = 3\\2x + 4y = 5\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x - 2y = 3\\ - x + 2y = - 2\end{array} \right.\).
Phương pháp giải:
Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình.
Lời giải chi tiết:
Sử dụng máy tính cầm tay, ta thấy hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 3\\2x + 4y = 5\end{array} \right.\) có nghiệm duy nhất là \(\left( {\frac{{11}}{4};\frac{{ - 1}}{8}} \right)\).
Chọn C
Trả lời câu hỏi Câu 7 trang 18 SBT Toán 9 Kết nối tri thức
Hệ phương trình \(\left\{ \begin{array}{l}3x - ay = b\\ax + by = 3\end{array} \right.\) có nghiệm là (2; -3) khi
A. \(a = 3,b = 3\).
B. \(a = 3,b = - 3\).
C. \(a = - 3,b = 3\).
D. \(a = - 3,b = - 3\).
Phương pháp giải:
+ Vì hệ phương trình có nghiệm là (2; -3) nên \(\left\{ \begin{array}{l}3.2 - a.\left( { - 3} \right) = b\\a.2 + b\left( { - 3} \right) = 3\end{array} \right.\)
+ Dùng máy tình cầm tay để tìm nghiệm của hệ phương trình thu được.
Lời giải chi tiết:
Vì hệ phương trình có nghiệm là (2; -3) nên \(\left\{ \begin{array}{l}3.2 - a.\left( { - 3} \right) = b\\a.2 + b\left( { - 3} \right) = 3\end{array} \right.\) hay \(\left\{ \begin{array}{l} - 3a + b = 6\\2a - 3b = 3\end{array} \right.\)
Sử dụng máy tính cầm tay, ta tìm được \(a = - 3;b = - 3\)
Chọn D
Trả lời câu hỏi Câu 8 trang 18 SBT Toán 9 Kết nối tri thức
Hệ phương trình \(\left\{ \begin{array}{l}x + my = 1\\ - mx - y = - 1\end{array} \right.\) có vô số nghiệm trong trường hợp nào sau đây?
A. \(m = 1\).
B. \(m = - 1\).
C. \(m = 2\).
D. \(m = - 2\).
Phương pháp giải:
Thay từng giá trị của m trong từng đáp án, ta thu được hệ hai phương trình bậc nhất hai ẩn, giải phương hệ trình đó để tìm đáp án đúng.
Lời giải chi tiết:
Với \(m = 1\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 1\\ - x - y = - 1\end{array} \right.\).
Cộng từng vế của hai phương trình trong hệ ta có: \(0x + 0y = 0\). Hệ thức này đúng với mọi giá trị của x và y.
Với giá trị tùy ý của y, giá trị của x được tính bằng \(x = 1 - y\).
Vậy hệ phương trình đã cho có nghiệm là \(\left( {1 - y;y} \right)\) với \(y \in \mathbb{R}\) tùy ý khi \(m = 1\).
Chọn A
Trả lời câu hỏi Câu 1 trang 17 SBT Toán 9 Kết nối tri thức
Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn?
A. \(\left\{ \begin{array}{l}2x + y = 3\\x - z = - 1\end{array} \right.\).
B. \(\left\{ \begin{array}{l}2x + y = 3\\0x + 0y = 1\end{array} \right.\).
C. \(\left\{ \begin{array}{l}2x + y = 3\\0x - y = - 1\end{array} \right.\).
D. \(\left\{ \begin{array}{l}2x + y = 3\\x + {y^2} = 1\end{array} \right.\).
Phương pháp giải:
Một cặp gồm hai phương trình bậc nhất hai ẩn \(ax + by = c\) và \(a'x + b'y = c'\) được gọi là một hệ phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (*).
Lời giải chi tiết:
Hệ \(\left\{ \begin{array}{l}2x + y = 3\\0x - y = - 1\end{array} \right.\) là hệ hai phương trình bậc nhất hai ẩn.
Chọn C
Trả lời câu hỏi Câu 2 trang 17 SBT Toán 9 Kết nối tri thức
Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x + 3y = - 1\\2x - y = 7\end{array} \right.\) là
A. (-1; 1).
B. (3; -1).
C. \(\left( {\frac{1}{2}; - 1} \right)\).
D. (2; -3).
Phương pháp giải:
Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình.
Lời giải chi tiết:
Sử dụng máy tính cầm tay, ta có nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x + 3y = - 1\\2x - y = 7\end{array} \right.\) là (2; -3).
Chọn D
Trả lời câu hỏi Câu 3 trang 18 SBT Toán 9 Kết nối tri thức
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 2), N(2; 3), P(-1; -1), Q(5; 8). Đường thẳng \(3x - 2y = - 1\) đi qua hai điểm nào trong các điểm đã cho?
A. M và N.
B. M và P.
C. P và Q.
D. N và P.
Phương pháp giải:
Nếu tại \(x = {x_0}\) và \(y = {y_0}\) ta có: \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì đường thẳng \(ax + by = c\) đi qua điểm A\(\left( {{x_0};{y_0}} \right)\).
Lời giải chi tiết:
Với \(x = 1,y = 2\) ta có: \(3.1 - 2.2 = - 1\) nên điểm M(1; 2) thuộc đường thẳng \(3x - 2y = - 1\).
Với \(x = 2,y = 3\) ta có: \(3.2 - 2.3 = 0 \ne - 1\) nên điểm N(2; 3) không thuộc đường thẳng \(3x - 2y = - 1\).
Với \(x = - 1,y = - 1\) ta có: \(3.\left( { - 1} \right) - 2.\left( { - 1} \right) = - 1\) nên điểm P(-1; -1) thuộc đường thẳng \(3x - 2y = - 1\).
Với \(x = 5,y = 8\) ta có: \(3.5 - 2.8 = - 1\) nên điểm Q(5; 8) thuộc đường thẳng \(3x - 2y = - 1\).
Vậy đường thẳng \(3x - 2y = - 1\) đi qua các điểm M, P, Q.
Chọn B, C
Trả lời câu hỏi Câu 4 trang 18 SBT Toán 9 Kết nối tri thức
Giá trị của a và b để đường thẳng \(y = ax + b\) đi qua hai điểm (1; -1) và (-1; 5) là
A. \(a = 1,b = - 2\).
B. \(a = - 5,b = 1\).
C. \(a = - 3,b = 2\).
D. \(a = - 1,b = 0\).
Phương pháp giải:
+ Vì đường thẳng \(y = ax + b\) đi qua hai điểm (1; -1) và (-1; 5) nên: \(\left\{ \begin{array}{l}a + b = - 1\\ - a + b = 5\end{array} \right.\)
+ Giải hệ phương trình vừa tìm được bằng phương pháp cộng đại số ta tìm được a, b.
Lời giải chi tiết:
Vì đường thẳng \(y = ax + b\) đi qua hai điểm (1; -1) và (-1; 5) nên: \(\left\{ \begin{array}{l}a + b = - 1\\ - a + b = 5\end{array} \right.\)
Cộng từng vế của hai phương trình trong hệ ta được: \(2b = 4\), suy ra \(b = 2\). Thay \(b = 2\) vào phương trình thứ nhất của hệ ta được: \(a + 2 = - 1\), suy ra \(a = - 3\).
Chọn C
Trả lời câu hỏi Câu 5 trang 18 SBT Toán 9 Kết nối tri thức
Hệ phương trình nào sau đây có nghiệm duy nhất?
A. \(\left\{ \begin{array}{l}x - 2y = 3\\2x - 4y = 5\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x - 2y = 3\\ - 2x + 4y = - 6\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x - 2y = 3\\2x + 4y = 5\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x - 2y = 3\\ - x + 2y = - 2\end{array} \right.\).
Phương pháp giải:
Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình.
Lời giải chi tiết:
Sử dụng máy tính cầm tay, ta thấy hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 3\\2x + 4y = 5\end{array} \right.\) có nghiệm duy nhất là \(\left( {\frac{{11}}{4};\frac{{ - 1}}{8}} \right)\).
Chọn C
Trả lời câu hỏi Câu 6 trang 18 SBT Toán 9 Kết nối tri thức
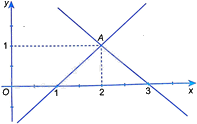
Hình bên dưới minh họa tập nghiệm của hệ phương trình nào sau đây?
A. \(\left\{ \begin{array}{l}x - y = 1\\x - y = 3\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x - y = 1\\x + y = 3\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x + y = 1\\x - y = 3\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x + y = 1\\x + y = 3\end{array} \right.\).
Phương pháp giải:
+ Từ hình vẽ ta thấy, hệ phương trình có một nghiệm duy nhất là (2; 1).
+ Dùng máy tính cầm tay để tính, ta tìm hệ phương trình nào có nghiệm duy nhất là (2; 1) thì đó là hệ phương trình cần tìm.
Lời giải chi tiết:
Từ hình vẽ ta thấy, hệ phương trình có một nghiệm duy nhất là (2; 1).
Sử dụng máy tính bỏ túi, ta thấy chỉ có hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\x + y = 3\end{array} \right.\) có nghiệm duy nhất là (2; 1).
Chọn B
Trả lời câu hỏi Câu 7 trang 18 SBT Toán 9 Kết nối tri thức
Hệ phương trình \(\left\{ \begin{array}{l}3x - ay = b\\ax + by = 3\end{array} \right.\) có nghiệm là (2; -3) khi
A. \(a = 3,b = 3\).
B. \(a = 3,b = - 3\).
C. \(a = - 3,b = 3\).
D. \(a = - 3,b = - 3\).
Phương pháp giải:
+ Vì hệ phương trình có nghiệm là (2; -3) nên \(\left\{ \begin{array}{l}3.2 - a.\left( { - 3} \right) = b\\a.2 + b\left( { - 3} \right) = 3\end{array} \right.\)
+ Dùng máy tình cầm tay để tìm nghiệm của hệ phương trình thu được.
Lời giải chi tiết:
Vì hệ phương trình có nghiệm là (2; -3) nên \(\left\{ \begin{array}{l}3.2 - a.\left( { - 3} \right) = b\\a.2 + b\left( { - 3} \right) = 3\end{array} \right.\) hay \(\left\{ \begin{array}{l} - 3a + b = 6\\2a - 3b = 3\end{array} \right.\)
Sử dụng máy tính cầm tay, ta tìm được \(a = - 3;b = - 3\)
Chọn D
Trả lời câu hỏi Câu 8 trang 18 SBT Toán 9 Kết nối tri thức
Hệ phương trình \(\left\{ \begin{array}{l}x + my = 1\\ - mx - y = - 1\end{array} \right.\) có vô số nghiệm trong trường hợp nào sau đây?
A. \(m = 1\).
B. \(m = - 1\).
C. \(m = 2\).
D. \(m = - 2\).
Phương pháp giải:
Thay từng giá trị của m trong từng đáp án, ta thu được hệ hai phương trình bậc nhất hai ẩn, giải phương hệ trình đó để tìm đáp án đúng.
Lời giải chi tiết:
Với \(m = 1\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 1\\ - x - y = - 1\end{array} \right.\).
Cộng từng vế của hai phương trình trong hệ ta có: \(0x + 0y = 0\). Hệ thức này đúng với mọi giá trị của x và y.
Với giá trị tùy ý của y, giá trị của x được tính bằng \(x = 1 - y\).
Vậy hệ phương trình đã cho có nghiệm là \(\left( {1 - y;y} \right)\) với \(y \in \mathbb{R}\) tùy ý khi \(m = 1\).
Chọn A
Trả lời câu hỏi Câu 6 trang 18 SBT Toán 9 Kết nối tri thức
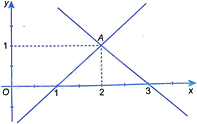
Hình bên dưới minh họa tập nghiệm của hệ phương trình nào sau đây?
A. \(\left\{ \begin{array}{l}x - y = 1\\x - y = 3\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x - y = 1\\x + y = 3\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x + y = 1\\x - y = 3\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x + y = 1\\x + y = 3\end{array} \right.\).
Phương pháp giải:
+ Từ hình vẽ ta thấy, hệ phương trình có một nghiệm duy nhất là (2; 1).
+ Dùng máy tính cầm tay để tính, ta tìm hệ phương trình nào có nghiệm duy nhất là (2; 1) thì đó là hệ phương trình cần tìm.
Lời giải chi tiết:
Từ hình vẽ ta thấy, hệ phương trình có một nghiệm duy nhất là (2; 1).
Sử dụng máy tính bỏ túi, ta thấy chỉ có hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\x + y = 3\end{array} \right.\) có nghiệm duy nhất là (2; 1).
Chọn B
Chương trình Toán 9 Kết nối tri thức tập 1 tập trung vào việc củng cố và mở rộng kiến thức về các biểu thức đại số, phương trình bậc nhất một ẩn, và các ứng dụng thực tế của chúng. Trang 17 và 18 của sách bài tập chứa các câu hỏi trắc nghiệm nhằm đánh giá khả năng vận dụng kiến thức của học sinh vào giải quyết các bài toán cụ thể. Việc giải các câu hỏi này không chỉ giúp học sinh làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng tư duy logic và khả năng phân tích vấn đề.
Dưới đây là phần giải chi tiết các câu hỏi trắc nghiệm trang 17, 18 sách bài tập Toán 9 - Kết nối tri thức tập 1:
Đề bài: (Giả định đề bài câu 1)...
Giải: (Giải thích chi tiết cách giải câu 1, bao gồm các bước thực hiện và lý giải tại sao lại chọn đáp án đó). Ví dụ: Để giải câu hỏi này, ta cần áp dụng công thức... Đáp án đúng là... vì...
Đề bài: (Giả định đề bài câu 2)...
Giải: (Giải thích chi tiết cách giải câu 2, bao gồm các bước thực hiện và lý giải tại sao lại chọn đáp án đó).
Đề bài: (Giả định đề bài câu 3)...
Giải: (Giải thích chi tiết cách giải câu 3, bao gồm các bước thực hiện và lý giải tại sao lại chọn đáp án đó).
Đề bài: (Giả định đề bài câu 4)...
Giải: (Giải thích chi tiết cách giải câu 4, bao gồm các bước thực hiện và lý giải tại sao lại chọn đáp án đó).
Các câu hỏi trắc nghiệm trong sách bài tập Toán 9 - Kết nối tri thức tập 1 thường xoay quanh các dạng bài sau:
Việc giải bài tập trắc nghiệm không chỉ giúp học sinh kiểm tra kiến thức mà còn rèn luyện các kỹ năng quan trọng như:
Hy vọng với bộ giải đáp chi tiết các câu hỏi trắc nghiệm trang 17, 18 sách bài tập Toán 9 - Kết nối tri thức tập 1, các em học sinh sẽ có thêm công cụ hỗ trợ học tập hiệu quả. Hãy luyện tập thường xuyên và áp dụng các mẹo giải bài tập để đạt kết quả tốt nhất trong các kỳ thi sắp tới. Chúc các em học tốt!