Bài 7.7 trang 26 sách bài tập Toán 9 Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song, vuông góc.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững phương pháp giải bài tập và tự tin hơn trong quá trình học tập.
Một túi chứa một số viên bi có cùng kích thước, mỗi viên bi có một trong các màu đen, trắng, đỏ, vàng. Thực hiện lấy bi 20 lần, mỗi lần lấy một viên xem viên bi có màu gì sau đó trả bi lại túi, trộn đều. Kết quả trong 20 lần lấy bi có 8 lần lấy được bi đen, 4 lần lấy được bi đỏ, 6 lần lấy được bi trắng, 2 lần lấy được bi vàng. a) Lập bảng tần số cho kết quả thu được. b) Vẽ biểu đồ tần số dạng cột biểu diễn bảng tần số thu được ở câu a.
Đề bài
Một túi chứa một số viên bi có cùng kích thước, mỗi viên bi có một trong các màu đen, trắng, đỏ, vàng. Thực hiện lấy bi 20 lần, mỗi lần lấy một viên xem viên bi có màu gì sau đó trả bi lại túi, trộn đều. Kết quả trong 20 lần lấy bi có 8 lần lấy được bi đen, 4 lần lấy được bi đỏ, 6 lần lấy được bi trắng, 2 lần lấy được bi vàng.
a) Lập bảng tần số cho kết quả thu được.
b) Vẽ biểu đồ tần số dạng cột biểu diễn bảng tần số thu được ở câu a.
Phương pháp giải - Xem chi tiết
a) Bảng tần số có dạng bảng sau:

Trong đó, \({m_1}\) là tần số của \({x_1}\), \({m_2}\) là tần số của \({x_2}\),…, \({m_k}\) là tần số của \({x_k}\).
Trong bảng tần số, ta chỉ liệt kê các giá trị \({x_i}\) khác nhau, các giá trị \({x_i}\) này có thể không là số.
b) Cách vẽ biểu đồ tần số dạng cột:
+ Vẽ hai trục ngang và dọc vuông góc với nhau, trục ngang: biểu thị các giá trị trong dãy dữ liệu, trục đứng: chọn khoảng chia thích hợp với dữ liệu và ghi ở các vạch chia.
+ Tại các vị trí đối tượng trên trục ngang, vẽ các cột hình chữ nhật: cách đều nhau, có cùng chiều rộng và chiều cao thể hiện tần số của các giá trị trong dãy dữ liệu, tương ứng với khoảng chia trên trục dọc.
+ Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ.
Lời giải chi tiết
a) Bảng tần số:

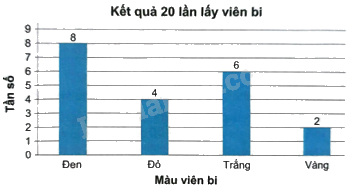
b) Biểu đồ:
Bài 7.7 trang 26 sách bài tập Toán 9 Kết nối tri thức tập 2 yêu cầu học sinh giải quyết các bài toán liên quan đến việc xác định đường thẳng song song, vuông góc và ứng dụng hàm số bậc nhất vào các tình huống thực tế. Dưới đây là hướng dẫn chi tiết từng bước để giải bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải bài 7.7 trang 26, chúng ta cần phân tích kỹ đề bài và xác định các yếu tố cần tìm. Thông thường, đề bài sẽ cung cấp thông tin về một đường thẳng và yêu cầu tìm đường thẳng thỏa mãn một điều kiện nào đó (song song, vuông góc, đi qua một điểm,...). Dưới đây là một ví dụ minh họa:
Ví dụ: Cho đường thẳng y = 2x - 1. Hãy tìm đường thẳng d:
a) Đường thẳng song song:
Vì đường thẳng d song song với y = 2x - 1 nên hệ số góc của d cũng là 2. Vậy phương trình đường thẳng d có dạng y = 2x + c. Thay tọa độ điểm A(1; 3) vào phương trình, ta được: 3 = 2 * 1 + c => c = 1. Vậy phương trình đường thẳng d là y = 2x + 1.
b) Đường thẳng vuông góc:
Vì đường thẳng d vuông góc với y = 2x - 1 nên hệ số góc của d là -1/2. Vậy phương trình đường thẳng d có dạng y = -1/2x + c. Thay tọa độ điểm B(-2; 0) vào phương trình, ta được: 0 = -1/2 * (-2) + c => c = -1. Vậy phương trình đường thẳng d là y = -1/2x - 1.
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể luyện tập thêm với các bài tập tương tự trong sách bài tập Toán 9 Kết nối tri thức tập 2. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải bài 7.7 trang 26 sách bài tập Toán 9 Kết nối tri thức tập 2 và đạt kết quả tốt trong môn Toán.