Bài 5.7 trang 59 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm hiểu và giải quyết các vấn đề cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho tam giác cân ABC (AB=AC). Gọi (O) là đường tròn đi qua ba điểm A, B, C và E là điểm trên cung nhỏ BC sao cho $oversetfrown{BE}=oversetfrown{EC}$. a) Chứng minh rằng ba điểm A, O, E thẳng hàng. b) Gọi H là chân đường cao hạ từ A xuống BC. Chứng minh rằng (AH < AB < AE).
Đề bài
Cho tam giác cân ABC (AB=AC). Gọi (O) là đường tròn đi qua ba điểm A, B, C và E là điểm trên cung nhỏ BC sao cho $\overset\frown{BE}=\overset\frown{EC}$.
a) Chứng minh rằng ba điểm A, O, E thẳng hàng.
b) Gọi H là chân đường cao hạ từ A xuống BC. Chứng minh rằng \(AH < AB < AE\).
Phương pháp giải - Xem chi tiết
a) + Chứng minh \(\Delta OAB = \Delta OAC\left( {c.c.c} \right)\). Suy ra \(\widehat {AOB} = \widehat {AOC}\), suy ra $\overset\frown{AB}=\overset\frown{AC}$
+ Mà $\overset\frown{BE}=\overset\frown{EC}$. Suy ra: sđ$\overset\frown{ABE}=sđ\overset\frown{ACE}$.
+ Vì $sđ\overset\frown{ABE}+sđ\overset\frown{ACE}={{360}^{o}}$ nên sđ$\overset\frown{ABE}=sđ\overset\frown{ACE}=\frac{{{360}^{o}}}{2}={{180}^{o}}$, suy ra ba điểm A, O, E thẳng hàng.
b) + Vì EA đi qua O nên AE là đường kính của (O), AB là dây không đi qua O nên \(AB < AE\).
+ Tam giác ABH vuông tại H nên AB là cạnh huyền. Do đó, \(AH < AB\).
+ Vậy \(AH < AB < AE\).
Lời giải chi tiết
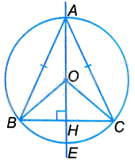
a) Tam giác OAB và tam giác OAC có: OA chung, \(AB = AC,OB = OC\) nên \(\Delta OAB = \Delta OAC\left( {c.c.c} \right)\).
Suy ra \(\widehat {AOB} = \widehat {AOC}\).
Mà AOB là góc ở tâm chắn cung nhỏ AB, AOC là góc ở tâm chắn cung nhỏ AC. Do đó, $\overset\frown{AB}=\overset\frown{AC}$
Theo giả thiết, $\overset\frown{BE}=\overset\frown{EC}$. Do đó, sđ$\overset\frown{AB}+sđ\overset\frown{BE}=sđ\overset\frown{EC}+sđ\overset\frown{AC}$
Suy ra: sđ$\overset\frown{ABE}=sđ\overset\frown{ACE}$. Mà $sđ\overset\frown{ABE}+sđ\overset\frown{ACE}={{360}^{o}}$ nên sđ$\overset\frown{ABE}=sđ\overset\frown{ACE}=\frac{{{360}^{o}}}{2}={{180}^{o}}$
Do đó, cung ABE là nửa đường tròn. Vậy ba điểm A, O, E thẳng hàng.
b) Vì EA đi qua O nên AE là đường kính của (O), AB là dây không đi qua O nên \(AB < AE\).
Tam giác ABH vuông tại H nên AB là cạnh huyền. Do đó, \(AH < AB\).
Vậy \(AH < AB < AE\).
Bài 5.7 trang 59 sách bài tập Toán 9 - Kết nối tri thức tập 1 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:
Nội dung bài tập 5.7:
Bài tập thường mô tả một tình huống thực tế, ví dụ như một vật thể chuyển động với vận tốc không đổi, hoặc một sự thay đổi tỉ lệ thuận giữa hai đại lượng. Học sinh cần xác định hàm số bậc nhất mô tả mối quan hệ đó và sử dụng hàm số để giải quyết các câu hỏi liên quan.
Để giải bài tập này, chúng ta thực hiện các bước sau:
Ví dụ minh họa:
Giả sử bài toán yêu cầu tìm hàm số biểu diễn quãng đường đi được của một ô tô với vận tốc 60km/h theo thời gian. Trong trường hợp này, quãng đường (s) là hàm số của thời gian (t), và hàm số có dạng s = 60t.
Nếu bài toán yêu cầu tính quãng đường ô tô đi được sau 2 giờ, ta chỉ cần thay t = 2 vào hàm số: s = 60 * 2 = 120km.
Ngoài bài tập 5.7, còn rất nhiều bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 1. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, học sinh nên luyện tập thêm các bài tập trong sách bài tập và các tài liệu tham khảo khác. Ngoài ra, học sinh có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học toán online để được hướng dẫn chi tiết và giải đáp thắc mắc.
Bảng tổng hợp các công thức liên quan:
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| (y - y1) / (x - x1) = (y2 - y1) / (x2 - x1) | Phương trình đường thẳng đi qua hai điểm |
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải bài tập 5.7 trang 59 sách bài tập Toán 9 - Kết nối tri thức tập 1 và các bài tập tương tự.