Bài 7.23 trang 37 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.23 trang 37, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Bảng tần số ghép nhóm sau cho biết thành tích luyện tập của một vận động viên nghiệp dư chạy maraton 42km. a) Lập bảng tần số tương đối ghép nhóm cho bảng thống kê trên. b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng biểu diễn bảng tần số tương đối ghép nhóm thu được.
Đề bài
Bảng tần số ghép nhóm sau cho biết thành tích luyện tập của một vận động viên nghiệp dư chạy maraton 42km.

a) Lập bảng tần số tương đối ghép nhóm cho bảng thống kê trên.
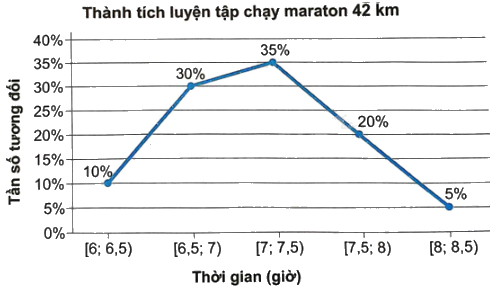
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng biểu diễn bảng tần số tương đối ghép nhóm thu được.
Phương pháp giải - Xem chi tiết
a) + Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối ghép nhóm:

b) Cách vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
Bước 1: Chọn giá trị \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) đại diện cho các nhóm số liệu \(\left[ {{a_i};{a_{i + 1}}} \right)\) với \(i = 1,2,3,..,k\).
Bước 2: Vẽ trục ngang để biểu diễn các giá trị đại diện cho nhóm số liệu, vẽ trục đứng thể hiện tần số tương đối.
Bước 3: Với mỗi giá trị đại diện \({x_i}\) trên trục ngang và tần số tương đối \({f_i}\) tương ứng, ta xác định một điểm \({M_i}\left( {{x_i};{f_i}} \right)\). Nối các điểm liên tiếp với nhau.
Bước 4: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ.
Lời giải chi tiết
a) Tổng số lần chạy của vận động viên là: \(2 + 6 + 7 + 4 + 1 = 20\).
Tần số tương đối của các nhóm [6; 6,5); [6,5; 7), [7; 7,5), [7,5; 8), [8; 8,5) lần lượt là:
\(\frac{2}{{20}}.100\% = 10\% ;\frac{6}{{20}}.100\% = 30\% ;\frac{7}{{20}}.100\% = 35\% ;\\\frac{4}{{20}}.100\% = 20\% ;\frac{1}{{20}}.100\% = 5\% \)
Bảng tần số tương đối ghép nhóm:

b) Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
Bài 7.23 thuộc chương trình Toán 9, tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất và hàm số bậc hai vào giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản sau:
Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Một người nông dân có một mảnh đất hình chữ nhật, chiều dài hơn chiều rộng 5m. Nếu tăng chiều dài thêm 2m và giảm chiều rộng đi 1m thì diện tích mảnh đất không đổi. Tính chiều dài và chiều rộng ban đầu của mảnh đất.)
Giải:
Thay x = y + 5 vào phương trình xy = (x + 2)(y - 1), ta được:
(y + 5)y = (y + 5 + 2)(y - 1)
y² + 5y = (y + 7)(y - 1)
y² + 5y = y² + 6y - 7
y = 7
Suy ra x = y + 5 = 7 + 5 = 12
Ngoài bài 7.23, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số để giải quyết các bài toán thực tế. Một số dạng bài tập thường gặp:
Để giải quyết các bài toán này, học sinh cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số, các em học sinh có thể tham khảo thêm các bài tập sau:
Bài 7.23 trang 37 Sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán ứng dụng của hàm số. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.