Bài 1.8 trang 8 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về giải phương trình bậc nhất một ẩn. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để tìm ra nghiệm của phương trình.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.8 trang 8 sách bài tập Toán 9 - Kết nối tri thức tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Bằng cách vẽ các đường thẳng thích hợp trên cùng một mặt phẳng tọa độ, hãy tìm nghiệm của mỗi hệ phương trình sau: a) (left{ begin{array}{l}2x = - 4\3x - y = 5end{array} right.); b) (left{ begin{array}{l}x - 2y = 4\2y = - 3end{array} right.).
Đề bài
Bằng cách vẽ các đường thẳng thích hợp trên cùng một mặt phẳng tọa độ, hãy tìm nghiệm của mỗi hệ phương trình sau:
a) \(\left\{ \begin{array}{l}2x = - 4\\3x - y = 5\end{array} \right.\);
b) \(\left\{ \begin{array}{l}x - 2y = 4\\2y = - 3\end{array} \right.\).
Phương pháp giải - Xem chi tiết
+ Biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn là đường thẳng \(ax + by = c\).
+ Nghiệm của hệ phương trình là giao điểm của hai đường thẳng đã biểu diễn ở trên.
Lời giải chi tiết
a) Đường thẳng (d): \(2x = - 4\) là đường thẳng song song với trục tung và cắt trục hoành tại điểm có hoành độ bằng -2.
Đường thẳng (d’): \(3x - y = 5\) đi qua hai điểm (0; -5) và \(\left( {\frac{5}{3};0} \right)\).
Vẽ hai đường thẳng (d) và (d’) trên cùng mặt phẳng tọa độ:
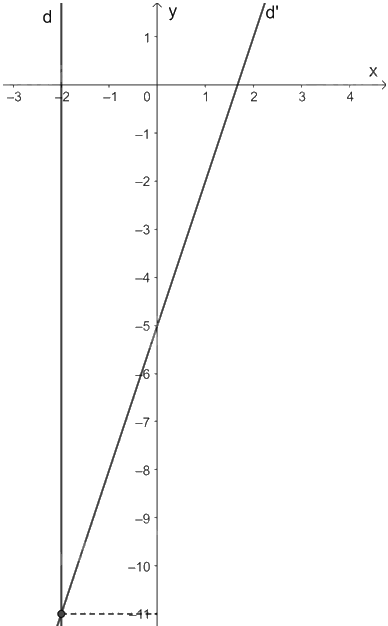
Từ đồ thị ta thấy, điểm (-2; -11) là nghiệm của hệ phương trình đã cho.
b) Đường thẳng (d): \(x - 2y = 4\) đi qua hai điểm A(0; -2) và B(4; 0).
Đường thẳng (d’): \(2y = - 3\) là đường thẳng song song với trục hoành và cắt trục tung tại điểm có tung độ \(y = - 1,5\).
Vẽ hai đường thẳng (d) và (d’) trên cùng mặt phẳng tọa độ:
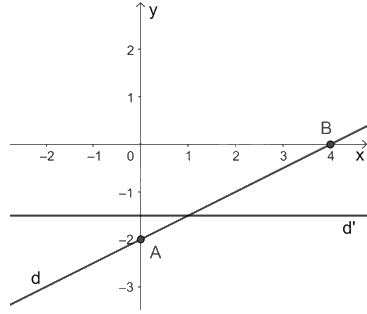
Từ đồ thị ta thấy, điểm (1; -1,5) là nghiệm của hệ phương trình đã cho.
Bài 1.8 trang 8 sách bài tập Toán 9 - Kết nối tri thức tập 1 yêu cầu giải các phương trình bậc nhất một ẩn. Để giải bài tập này, chúng ta cần nắm vững các bước sau:
Dưới đây là lời giải chi tiết cho từng phương trình trong bài 1.8 trang 8 sách bài tập Toán 9 - Kết nối tri thức tập 1:
3x + 9 = 0
3x = -9
x = -9/3
x = -3
-5x + 15 = 0
-5x = -15
x = -15/-5
x = 3
2x - 10 = 0
2x = 10
x = 10/2
x = 5
-7x - 14 = 0
-7x = 14
x = 14/-7
x = -2
Phương trình bậc nhất một ẩn có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về giải phương trình bậc nhất một ẩn, bạn có thể luyện tập thêm các bài tập sau:
Hy vọng với lời giải chi tiết và những lưu ý quan trọng trên, các em học sinh sẽ tự tin hơn khi giải bài 1.8 trang 8 sách bài tập Toán 9 - Kết nối tri thức tập 1 và các bài tập tương tự. Chúc các em học tốt!