Bài 9.30 trang 56 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.30, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình thoi ABCD có AC=8cm, BD=4cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác MNPQ nội tiếp một đường tròn và tìm bán kính của đường tròn đó.
Đề bài
Cho hình thoi ABCD có AC=8cm, BD=4cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác MNPQ nội tiếp một đường tròn và tìm bán kính của đường tròn đó.
Phương pháp giải - Xem chi tiết
+ Gọi O là giao điểm của AC và BD.
+ Tính được OA, OB, OC, OD và chỉ ra AC vuông góc với BD tại O.
+ Chứng minh M là tâm đường tròn ngoại tiếp tam giác OAB, từ đó tính được MO.
+ Chứng minh được \(MO = NO = PO = OQ\) nên tứ giác MNPQ nội tiếp đường tròn (O) bán kính MO.
Lời giải chi tiết
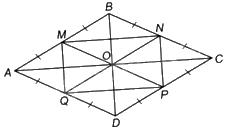
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình thoi nên \(OA = OC = \frac{1}{2}AC = 4cm,OB = OD = \frac{1}{2}BD = 2cm\) và AC vuông góc với BD tại O.
Áp dụng định lí Pythagore vào tam giác ABO vuông tại O có: \(A{B^2} = O{A^2} + O{B^2} = 20\) nên \(AB = 2\sqrt 5 cm\).
Do đó, \(AB = BC = CD = DA = 2\sqrt 5 cm\).
Vì M là trung điểm của AB, tam giác AOB vuông tại O nên M là tâm đường tròn ngoại tiếp tam giác OAB và \(MO = MA = MB = \frac{{AB}}{2} = \sqrt 5 cm\).
Tương tự ta có: \(MO = NO = PO = OQ = \sqrt 5 cm\).
Vậy tứ giác MNPQ nội tiếp đường tròn (O) bán kính \(\sqrt 5 cm\).
Bài 9.30 sách bài tập Toán 9 - Kết nối tri thức tập 2 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc nhất và ứng dụng thực tế. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số, đặc biệt là cách xác định hệ số góc và tung độ gốc.
Trước khi bắt đầu giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 9.30, đề bài thường đưa ra một tình huống thực tế và yêu cầu chúng ta xây dựng hàm số mô tả mối quan hệ giữa các đại lượng trong tình huống đó. Sau đó, chúng ta cần sử dụng hàm số vừa xây dựng để trả lời các câu hỏi cụ thể của bài toán.
Đề bài: Một người đi xe đạp từ A đến B với vận tốc không đổi là 15 km/h. Hãy viết hàm số biểu thị quãng đường đi được của người đó theo thời gian đi.
Giải:
Vậy hàm số biểu thị quãng đường đi được của người đó theo thời gian đi là y = 15x.
Để hiểu sâu hơn về hàm số và ứng dụng của chúng, bạn có thể tham khảo thêm các kiến thức sau:
Để củng cố kiến thức, bạn có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2. Ngoài ra, bạn có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Bài 9.30 trang 56 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán và ứng dụng kiến thức vào thực tế. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.