Bài 6.26 trang 17 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.26 trang 17, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Hình chữ nhật vàng là hình chữ nhật có thể chia thành một hình vuông và hình chữ nhật thứ hai có các kích thước tỉ lệ với các kích thước tương ứng của hình chữ nhật ban đầu (với cùng hệ số tỉ lệ). Tỉ số x giữa chiều dài và chiều rộng của hình chữ nhật vàng được gọi là tỉ lệ vàng. a) Tính tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD và hình chữ nhật EBCF. b) Tìm giá trị chính xác của tỉ lệ vàng bằng cách đặt hai tỉ số ở câu a bằng nhau rồi tìm x.
Đề bài
Hình chữ nhật vàng là hình chữ nhật có thể chia thành một hình vuông và hình chữ nhật thứ hai có các kích thước tỉ lệ với các kích thước tương ứng của hình chữ nhật ban đầu (với cùng hệ số tỉ lệ). Tỉ số x giữa chiều dài và chiều rộng của hình chữ nhật vàng được gọi là tỉ lệ vàng.
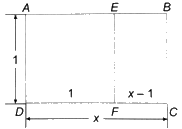
a) Tính tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD và hình chữ nhật EBCF.
b) Tìm giá trị chính xác của tỉ lệ vàng bằng cách đặt hai tỉ số ở câu a bằng nhau rồi tìm x.
Phương pháp giải - Xem chi tiết
a) Giả sử hình chữ nhật ABCD có chiều rộng \(AD = BC = 1cm\) và chiều dài \(AB = CD = x\left( {cm} \right)\). Điều kiện \(x > 1\) nên tính được tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD.
+ Chiều dài của hình chữ nhật EBCF là \(AD = EF = 1cm\) và chiều rộng là \(EB = FC = x - 1\left( {cm} \right)\), từ đó tính được tỉ số giữa chiều dài và chiều rộng của hình chữ nhật EBCF.
b) + Theo đề bài ta có phương trình: \(\frac{x}{1} = \frac{1}{{x - 1}}\).
+ Giải phương trình thu được, kết hợp với điều kiện và đưa ra kết luận.
Lời giải chi tiết
a) Giả sử hình chữ nhật ABCD có chiều rộng \(AD = BC = 1cm\) và chiều dài \(AB = CD = x\left( {cm} \right)\). Điều kiện \(x > 1\). Do đó tỉ số giữa chiều dài và chiều rộng của hình chữ nhật ABCD là \(\frac{x}{1}\).
Từ hình vẽ ta thấy chiều dài của hình chữ nhật EBCF là \(AD = EF = 1cm\) và chiều rộng là \(EB = FC = x - 1\left( {cm} \right)\). Do đó, tỉ số chiều dài và chiều rộng của hình chữ nhật EBCF là: \(\frac{1}{{x - 1}}\).
b) Theo đề bài ta có phương trình: \(\frac{x}{1} = \frac{1}{{x - 1}}\)
Nhân hai vế của phương trình này với \(x - 1\) để khử mẫu ta được \(x\left( {x - 1} \right) = 1\) hay \({x^2} - x - 1 = 0\).
Ta có: \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 1} \right) = 5\) nên phương trình có hai nghiệm \({x_1} = \frac{{1 + \sqrt 5 }}{2}\) (thỏa mãn) và \({x_2} = \frac{{1 - \sqrt 5 }}{2}\) (không thỏa mãn).
Vậy tỉ lệ vàng là \(\frac{{1 + \sqrt 5 }}{2}\).
Bài 6.26 thuộc chương trình Toán 9, tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất và hàm số bậc hai vào giải quyết các bài toán thực tế. Để giải bài tập này hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Một người đi xe máy từ A đến B với vận tốc 40km/h. Nếu tăng vận tốc thêm 5km/h thì thời gian đi từ A đến B giảm đi 18 phút. Tính quãng đường AB.)
Lời giải:
Quy đồng mẫu số, ta được: 9x - 8x = 120
=> x = 120
Ngoài bài 6.26, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số để giải quyết các bài toán thực tế. Một số dạng bài tập thường gặp:
Để giải các bài tập này, học sinh cần:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo thêm các bài tập sau:
Bài 6.26 trang 17 Sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán ứng dụng hàm số. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài toán tương tự.