Bài 5.17 trang 65 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và ứng dụng thực tế để giải quyết các vấn đề liên quan.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.17 trang 65, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho đường tròn (O) và điểm P. a) Giả sử (P in left( O right)). Vẽ đường thẳng a đi qua P và vuông góc với OP. Chứng minh rằng a là tiếp tuyến của đường tròn (O) tại P. b) Giả sử P nằm ngoài (O). Vẽ đường tròn đường kính OP. Đường tròn vừa vẽ cắt (O) tại A và B. Chứng minh rằng PA và PB là hai tiếp tuyến của (O).
Đề bài
Cho đường tròn (O) và điểm P.
a) Giả sử \(P \in \left( O \right)\). Vẽ đường thẳng a đi qua P và vuông góc với OP. Chứng minh rằng a là tiếp tuyến của đường tròn (O) tại P.
b) Giả sử P nằm ngoài (O). Vẽ đường tròn đường kính OP. Đường tròn vừa vẽ cắt (O) tại A và B. Chứng minh rằng PA và PB là hai tiếp tuyến của (O).
Phương pháp giải - Xem chi tiết
a) Vì \(P \in \left( O \right)\) và \(a \bot OP\) tại P nên a là tiếp tuyến của đường tròn (O) tại P.
b) + Gọi I là trung điểm của OP. Suy ra, bốn điểm O, A, P, B thuộc đường tròn tâm I, đường kính OP.
+ Chứng minh tam giác OBP vuông tại B, suy ra \(OB \bot BP\) tại B, suy ra PB là tiếp tuyến của (O) tại B.
+ Chứng minh tam giác OAP vuông tại A, do đó \(OA \bot AP\) tại A, suy ra PA là tiếp tuyến của (O) tại A.
Lời giải chi tiết
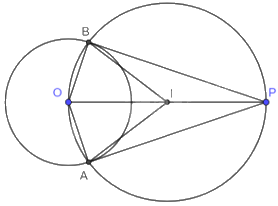
a) Vì \(P \in \left( O \right)\) và \(a \bot OP\) tại P nên a là tiếp tuyến của đường tròn (O) tại P.
b) Gọi I là trung điểm của OP. Suy ra, bốn điểm O, A, P, B thuộc đường tròn tâm I, đường kính OP.
Tam giác OBP có BI là đường trung tuyến và \(BI = IP = OI = \frac{1}{2}OP\) nên tam giác OBP vuông tại B. Do đó, \(OB \bot BP\) tại B.
Vì B thuộc (O) và \(OB \bot BP\) tại B nên PB là tiếp tuyến của (O) tại B.
Tam giác OAP có AI là đường trung tuyến và \(AI = IP = OI = \frac{1}{2}OP\) nên tam giác OAP vuông tại A. Do đó, \(OA \bot AP\) tại A.
Vì A thuộc (O) và \(OA \bot AP\) tại A nên PA là tiếp tuyến của (O) tại A.
Trước khi đi vào giải chi tiết bài 5.17, chúng ta cùng ôn lại một số kiến thức lý thuyết quan trọng liên quan đến hàm số bậc nhất và ứng dụng thực tế. Hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc. Việc hiểu rõ ý nghĩa của a và b giúp chúng ta phân tích và giải quyết các bài toán liên quan một cách hiệu quả.
Bài 5.17 yêu cầu chúng ta giải một bài toán thực tế liên quan đến việc xác định hàm số bậc nhất biểu diễn mối quan hệ giữa hai đại lượng. Để giải bài toán này, chúng ta cần:
Đề bài: (Nội dung đề bài cụ thể sẽ được chèn vào đây - ví dụ: Một người đi xe đạp với vận tốc không đổi là 15 km/h. Hãy viết hàm số biểu thị quãng đường đi được của người đó theo thời gian.)
Giải:
Gọi x là thời gian người đó đi xe đạp (đơn vị: giờ) và y là quãng đường người đó đi được (đơn vị: km). Ta có hàm số y = 15x.
Hàm số y = 15x là một hàm số bậc nhất với hệ số góc a = 15 và tung độ gốc b = 0. Đồ thị của hàm số là một đường thẳng đi qua gốc tọa độ và có độ dốc là 15.
Để hiểu rõ hơn về cách giải bài toán này, chúng ta cùng xét một ví dụ minh họa khác. (Nội dung ví dụ minh họa sẽ được chèn vào đây). Sau đó, chúng ta sẽ giải một số bài tập tương tự để củng cố kiến thức.
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 5.17 trang 65 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng thực tế. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ nắm vững kiến thức và tự tin làm bài tập.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| a | Hệ số góc |
| b | Tung độ gốc |