Bài 4.29 trang 51 sách bài tập toán 9 thuộc chương trình Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về cách xác định hệ số góc và tung độ gốc của hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.29 trang 51 sách bài tập toán 9, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Xét điểm B nằm giữa hai điểm A và H. Giả sử có điểm D sao cho DH vuông góc với AB và (widehat {DAH} = {15^o},widehat {DBH} = {30^o}). Chứng minh rằng (HD = frac{{AB}}{2}).
Đề bài
Xét điểm B nằm giữa hai điểm A và H. Giả sử có điểm D sao cho DH vuông góc với AB và \(\widehat {DAH} = {15^o},\widehat {DBH} = {30^o}\). Chứng minh rằng \(HD = \frac{{AB}}{2}\).
Phương pháp giải - Xem chi tiết
+ Tam giác HDB vuông tại H nên \(\frac{{HD}}{{BD}} = \sin \widehat {HBD}\).
+ Tính được góc ADB của tam giác ABD, từ đó suy ra tam giác ABD cân tại D nên \(BD = AB\).
+ Do đó, \(BD = AB = 2HD\), suy ra điều phải chứng minh.
Lời giải chi tiết
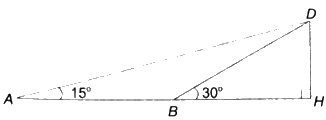
Tam giác HDB vuông tại H nên \(\frac{{HD}}{{BD}} = \sin \widehat {HBD} = \sin {30^o} = \frac{1}{2}\) nên \(BD = 2HD\).
Tam giác ABD có \(\widehat {ABD} = {180^o} - \widehat {DBH} = {150^o},\) \(\widehat {BAD} = {15^o}\) nên \(\widehat {ADB} = {180^o} - \widehat {ABD} - \widehat A = {15^o}\).
Do đó tam giác ABD cân tại B. Suy ra \(BD = AB\).
Suy ra \(BD = AB = 2HD\) nên \(HD = \frac{{AB}}{2}\).
Cho hàm số y = (m - 1)x + 3. Tìm giá trị của m để hàm số đồng biến và đi qua điểm A(1; 2).
Để hàm số y = (m - 1)x + 3 đồng biến, hệ số góc của hàm số phải lớn hơn 0. Do đó:
m - 1 > 0
m > 1
Hàm số đi qua điểm A(1; 2) nên tọa độ của điểm A phải thỏa mãn phương trình của hàm số. Thay x = 1 và y = 2 vào phương trình, ta được:
2 = (m - 1) * 1 + 3
2 = m - 1 + 3
2 = m + 2
m = 0
Tuy nhiên, điều kiện để hàm số đồng biến là m > 1. Vậy m = 0 không thỏa mãn điều kiện này.
Kết luận: Không có giá trị nào của m thỏa mãn cả hai điều kiện trên.
Bài toán này yêu cầu học sinh kết hợp kiến thức về hàm số bậc nhất và điều kiện đồng biến của hàm số. Để giải bài toán, học sinh cần:
Trong quá trình giải bài toán, học sinh cần chú ý kiểm tra điều kiện của tham số để đảm bảo nghiệm tìm được thỏa mãn tất cả các yêu cầu của bài toán.
Để củng cố kiến thức về hàm số bậc nhất và điều kiện đồng biến, học sinh có thể tham khảo các bài tập tương tự sau:
Hàm số bậc nhất là một khái niệm quan trọng trong toán học, được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Việc nắm vững kiến thức về hàm số bậc nhất sẽ giúp học sinh giải quyết các bài toán phức tạp hơn trong tương lai.
Ngoài ra, học sinh cũng nên tìm hiểu về các loại hàm số khác như hàm số bậc hai, hàm số mũ, hàm số logarit để có cái nhìn toàn diện hơn về toán học.
Khi giải bài tập về hàm số bậc nhất, học sinh cần:
| Công thức | Mô tả |
|---|---|
| y = ax + b | Phương trình hàm số bậc nhất, trong đó a là hệ số góc, b là tung độ gốc. |
| a > 0 | Hàm số đồng biến. |
| a < 0 | Hàm số nghịch biến. |
Hy vọng với lời giải chi tiết và những phân tích trên, các em học sinh đã hiểu rõ cách giải bài 4.29 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 1. Chúc các em học tập tốt!