Giải bài 4.35 trang 52 Sách bài tập Toán 9 - Kết nối tri thức tập 1

Giải bài 4.35 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1

Giải bài 4.35 trang 52 Sách bài tập Toán 9 - Kết nối tri thức tập 1

Bài 4.35 trang 52 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và ứng dụng thực tế để giải quyết vấn đề.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.35 trang 52, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

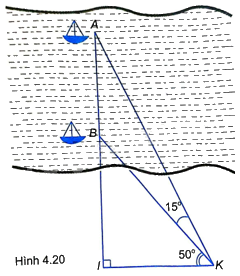
Hai chiếc thuyền A và B ở vị trí được minh họa như trong Hình 4.20. Tính khoảng cách giữa chúng (làm tròn đến m), biết (IK = 380m).

Đề bài

Hai chiếc thuyền A và B ở vị trí được minh họa như trong Hình 4.20. Tính khoảng cách giữa chúng (làm tròn đến m), biết \(IK = 380m\).

Giải bài 4.35 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1 1

Phương pháp giải - Xem chi tiết Giải bài 4.35 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1 2

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối.

Lời giải chi tiết

Trong tam giác AIK vuông tại I nên \(IA = IK.\tan \widehat {AKI} = IK.\tan {65^o}\).

Trong tam giác BIK vuông tại I nên \(IB = IK.\tan \widehat {BKI} = IK.\tan {50^o}\).

Do đó, \(AB = AI - IB = IK\left( {\tan {{65}^o} - \tan {{50}^o}} \right) \) \(= 380\left( {\tan {{65}^o} - \tan {{50}^o}} \right) \approx 362\left( m \right)\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 4.35 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1 đặc sắc thuộc chuyên mục giải bài tập toán lớp 9 trên nền tảng toán học. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 4.35 trang 52 Sách bài tập Toán 9 - Kết nối tri thức tập 1: Hướng dẫn chi tiết

Bài 4.35 trang 52 sách bài tập Toán 9 Kết nối tri thức tập 1 yêu cầu chúng ta giải quyết một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài này, chúng ta cần nắm vững các kiến thức sau:

Hàm số bậc nhất: Dạng y = ax + b (a ≠ 0).
Đồ thị hàm số bậc nhất: Đường thẳng đi qua hai điểm.
Ứng dụng của hàm số bậc nhất: Giải quyết các bài toán thực tế.

Nội dung bài toán: (Giả sử bài toán có nội dung cụ thể về một tình huống thực tế, ví dụ: một người đi xe đạp với vận tốc không đổi, quãng đường đi được theo thời gian, v.v.)

Lời giải:

Bước 1: Xác định hàm số. Dựa vào thông tin đề bài, ta xác định được hàm số mô tả mối quan hệ giữa các đại lượng. Ví dụ, nếu đề bài cho vận tốc và thời gian, ta có thể xác định hàm số biểu diễn quãng đường đi được.
Bước 2: Tìm các hệ số của hàm số. Sử dụng các dữ kiện đề bài cung cấp để tìm các hệ số a và b trong hàm số y = ax + b.
Bước 3: Giải các câu hỏi của bài toán. Sử dụng hàm số đã tìm được để trả lời các câu hỏi của bài toán. Ví dụ, tính quãng đường đi được sau một khoảng thời gian nhất định, hoặc tìm thời gian cần thiết để đi được một quãng đường nhất định.

Ví dụ minh họa:

(Giả sử bài toán cụ thể và lời giải chi tiết được trình bày ở đây, bao gồm các bước tính toán, giải thích rõ ràng và kết quả cuối cùng.)

Lưu ý:

Khi giải bài toán, cần đọc kỹ đề bài và xác định rõ các đại lượng liên quan.
Sử dụng các kiến thức đã học về hàm số bậc nhất để xây dựng phương trình và giải quyết bài toán.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài tập tương tự:

(Liệt kê một số bài tập tương tự để học sinh luyện tập và củng cố kiến thức.)

Tổng kết:

Bài 4.35 trang 52 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập ứng dụng quan trọng, giúp học sinh hiểu rõ hơn về hàm số bậc nhất và khả năng ứng dụng của nó trong thực tế. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp các em học sinh tự tin hơn trong quá trình học tập môn Toán.

Các kiến thức liên quan

Hàm số bậc nhất
Đồ thị hàm số bậc nhất
Ứng dụng hàm số bậc nhất

Giaitoan.edu.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài 4.35 trang 52 sách bài tập Toán 9 Kết nối tri thức tập 1 và đạt kết quả tốt trong học tập.