Bài 7.29 trang 41 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.29, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Thành tích ném lao của 40 vận động viên nam trong giải thể thao trên được cho như sau: a) Lập bảng tần số tương đối ghép nhóm. b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột biểu diễn bảng tần số tương đối ghép nhóm thu được ở câu a. c) Từ biểu đồ thu được ở câu b và biểu đồ cho trong bài tập 7.28, hãy nhận xét và thành tích ném lao của các vận động viên nam và nữ.
Đề bài
Thành tích ném lao của 40 vận động viên nam trong giải thể thao trên được cho như sau:

a) Lập bảng tần số tương đối ghép nhóm.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột biểu diễn bảng tần số tương đối ghép nhóm thu được ở câu a.
c) Từ biểu đồ thu được ở câu b và biểu đồ cho trong bài tập 7.28, hãy nhận xét và thành tích ném lao của các vận động viên nam và nữ.
Phương pháp giải - Xem chi tiết
a) Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối ghép nhóm:

b) Cách vẽ biểu đồ tần số tương đối ghép nhóm dạng cột:
Bước 1: Vẽ trục đứng, trục ngang. Trên trục đứng xác định đơn vị độ dài phù hợp với các tần số tương đối. Trên trục ngang xác định các nhóm số liệu cần biểu diễn.
Bước 2: Dựng các hình cột (kề nhau) ứng với các nhóm dữ liệu, mỗi hình cột có chiều cao bằng tần số tương đối của nhóm số liệu.
Bước 3: Ghi chú giải cho các trục, các cột và tiêu đề cho biểu đồ.
c) Từ biểu đồ bài 7.28 và 7.29 ta rút ra kết luận: Thành tích ném lao của vận động viên nam cao hơn vận động viên nữ.
Lời giải chi tiết
a) Tần số tương đối ứng với các nhóm [70,5; 71), [71; 71,5), [71,5; 72), [72; 72,5), [72,5; 73), [73; 73,5) tương ứng là:
\(\frac{2}{{40}}.100\% = 5\% ;\frac{5}{{40}}.100\% = 12,5\% ;\frac{7}{{40}}.100\% = 17,5\% ;\)
\(\frac{{15}}{{40}}.100\% = 37,5\% ;\frac{8}{{40}}.100\% = 20\% ,\frac{3}{{40}}.100\% = 7,5\% \).
Ta có bảng tần số tương đối như sau:

b) Biểu đồ tần số tương đối ghép nhóm dạng cột:
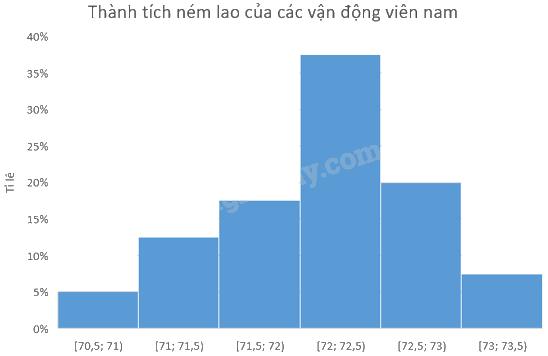
c) Thành tích ném lao của vận động viên nam cao hơn vận động viên nữ.
Bài 7.29 thuộc chương trình Toán 9, tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất và hàm số bậc hai vào giải quyết các bài toán thực tế. Để giải bài tập này hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Một người đi xe máy từ A đến B với vận tốc 40km/h. Nếu người đó tăng vận tốc thêm 5km/h thì sẽ đến B sớm hơn 10 phút. Tính quãng đường AB.)
Lời giải:
Phương trình: x/40 - x/45 = 1/6
Quy đồng mẫu số: 9x - 8x = 60
Giải phương trình: x = 60
Ngoài bài 7.29, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số và phương trình để giải quyết các vấn đề thực tế. Một số dạng bài tập thường gặp:
Để giải các bài tập này, học sinh cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số và phương trình, học sinh nên luyện tập thêm các bài tập trong sách bài tập, sách giáo khoa và các đề thi thử. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp các em học sinh rèn luyện và nâng cao khả năng giải toán.
Ngoài sách giáo khoa và sách bài tập, học sinh có thể tham khảo thêm các tài liệu sau:
Học toán đòi hỏi sự kiên trì, chăm chỉ và phương pháp học tập đúng đắn. Hãy dành thời gian ôn tập lý thuyết, luyện tập bài tập thường xuyên và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học sinh học tốt môn Toán!