Bài 5.4 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học toán lớp 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.4 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 1). Gọi B, C và D là các điểm đối xứng với A lần lượt qua trục hoành, qua gốc O và qua trục tung. a) Xác định tọa độ của ba điểm B, C và D. b) Có hay không một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm và bán kính của đường tròn đó, nếu có.
Đề bài
Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 1). Gọi B, C và D là các điểm đối xứng với A lần lượt qua trục hoành, qua gốc O và qua trục tung.
a) Xác định tọa độ của ba điểm B, C và D.
b) Có hay không một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm và bán kính của đường tròn đó, nếu có.
Phương pháp giải - Xem chi tiết
a) - Vì B đối xứng với A qua trục hoành nên:
+ AB vuông góc với Ox, suy ra A và B có cùng hoành độ.
+ A và B cách đều Ox, nên A và B có tung độ đối nhau.
- Vì C đối xứng với A qua gốc O nên O là trung điểm của AC. Do đó, A và C có hoành độ và tung độ đối nhau.
- Vì D đối xứng với A qua trục tung nên:
+ AD vuông góc với Oy, suy ra A và D có cùng tung độ.
+ A và D cách đều Oy, nên A và D có hoành độ đối nhau.
b) + Gọi H là hình chiếu của D trên trục Ox. Khi đó, H(-3; 0) và DH vuông góc với OH.
+ Áp dụng định lí Pythagore vào tam giác DOH vuông tại H tính được \(OD = \sqrt {10} \)
+ Tương tự ta tính được \(OA = OB = OC = \sqrt {10} \)
+ Vì \(OA = OB = OC = OD = \sqrt {10} \) nên bốn điểm A, B, C và D cùng thuộc đường tròn (O, \(\sqrt {10} \)).
Lời giải chi tiết
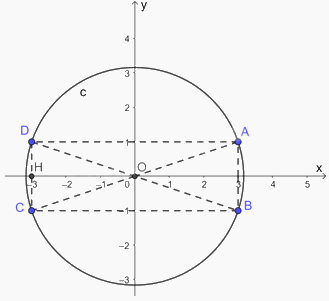
a) Vì B đối xứng với A qua trục hoành nên:
+ AB vuông góc với Ox, suy ra A và B có cùng hoành độ.
+ A và B cách đều Ox, nên A và B có tung độ đối nhau.
Suy ra: B(3; -1)
Vì C đối xứng với A qua gốc O nên O là trung điểm của AC. Do đó, A và C có hoành độ và tung độ đối nhau. Suy ra C(-3; -1).
Vì D đối xứng với A qua trục tung nên:
+ AD vuông góc với Oy, suy ra A và D có cùng tung độ.
+ A và D cách đều Oy, nên A và D có hoành độ đối nhau.
Suy ra D(-3; 1).
b) Gọi H là hình chiếu của D trên trục Ox. Khi đó, H(-3; 0) và DH vuông góc với OH.
Áp dụng định lí Pythagore vào tam giác DOH vuông tại H ta có: \(O{D^2} = D{H^2} + O{H^2} = {1^2} + {3^2} = 10\) nên \(OD = \sqrt {10} \).
Tương tự ta có: \(OA = OB = OC = \sqrt {10} \).
Vì \(OA = OB = OC = OD = \sqrt {10} \) nên bốn điểm A, B, C và D cùng thuộc đường tròn (O, \(\sqrt {10} \)).
Bài 5.4 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1 thuộc chương trình học toán lớp 9, tập trung vào việc ứng dụng hệ phương trình bậc nhất hai ẩn vào giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Dưới đây là hướng dẫn chi tiết cách giải bài 5.4 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1:
Một người đi xe máy từ A đến B với vận tốc 40km/h. Nếu người đó tăng vận tốc thêm 5km/h thì sẽ đến B sớm hơn 18 phút. Tính quãng đường AB.
1. Đặt ẩn:
2. Lập phương trình:
3. Giải hệ phương trình:
Ta có phương trình: x/40 - x/45 = 0.3
Quy đồng mẫu số: 9x - 8x = 0.3 * 360
Giải phương trình: x = 108
4. Kết luận:
Quãng đường AB là 108km.
Bài tập 5.4 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1 là một ví dụ điển hình về ứng dụng hệ phương trình vào giải quyết các bài toán thực tế. Việc nắm vững kiến thức và kỹ năng giải hệ phương trình sẽ giúp học sinh giải quyết các bài toán tương tự một cách dễ dàng và hiệu quả.
Để củng cố kiến thức về hệ phương trình và ứng dụng vào giải bài toán thực tế, học sinh có thể tham khảo các bài tập tương tự sau:
Giaitoan.edu.vn hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ cách giải bài 5.4 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1 và tự tin hơn trong quá trình học tập môn toán.
Ngoài ra, các em có thể tham khảo thêm các bài giảng và tài liệu học tập khác trên Giaitoan.edu.vn để nâng cao kiến thức và kỹ năng giải toán.