Bài 5.25 trang 68 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.25 trang 68, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho I là trung điểm của đoạn AB. Xét các đường tròn (I; IB) và (A; AB). a) Hai đường tròn (I) và (A) nói trên có vị trí tương đối như thế nào? b) Đường thẳng đi qua B, cắt các đường tròn (I) và (A) lần lượt tại C và D. Hãy so sánh các độ dài BC và CD.
Đề bài
Cho I là trung điểm của đoạn AB. Xét các đường tròn (I; IB) và (A; AB).
a) Hai đường tròn (I) và (A) nói trên có vị trí tương đối như thế nào?
b) Đường thẳng đi qua B, cắt các đường tròn (I) và (A) lần lượt tại C và D. Hãy so sánh các độ dài BC và CD.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(IA = AB - IB\) nên hai đường tròn (I; IB) và (A; AB) tiếp xúc trong.
b) + Chứng minh tam giác ACB vuông tại C, suy ra \(AC \bot CB\).
+ Chứng minh tam giác ABD cân tại A. Do đó, AC là đường cao đồng thời là đường trung tuyến trong tam giác ABD. Do đó, \(BC = CD\).
Lời giải chi tiết
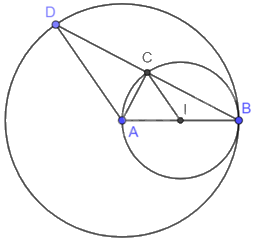
a) Vì I thuộc AB nên \(IA = AB - IB\) nên hai đường tròn (I; IB) và (A; AB) tiếp xúc trong.
b) Tam giác ABC có CI là đường trung tuyến và \(CI = IA = IB = \frac{1}{2}AB\) nên tam giác ACB vuông tại C. Do đó, \(AC \bot CB\).
Vì AB = AD (bằng bán kính của (A; AB)) nên tam giác ABD cân tại A.
Do đó, AC là đường cao đồng thời là đường trung tuyến trong tam giác ABD. Do đó, \(BC = CD\).
Bài 5.25 trang 68 sách bài tập Toán 9 Kết nối tri thức tập 1 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc nhất và hàm số bậc hai. Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết bài 5.25 trang 68:
Một người đi xe máy từ A đến B với vận tốc trung bình 40 km/h. Nếu người đó tăng vận tốc thêm 5 km/h thì sẽ đến B sớm hơn 18 phút. Tính quãng đường AB.
Gọi quãng đường AB là x (km). Thời gian người đó đi từ A đến B với vận tốc 40 km/h là x/40 (giờ). Nếu người đó tăng vận tốc thêm 5 km/h, vận tốc mới là 45 km/h. Thời gian người đó đi từ A đến B với vận tốc 45 km/h là x/45 (giờ).
Vì người đó đến B sớm hơn 18 phút, ta có phương trình:
x/40 - x/45 = 18/60
Quy đồng mẫu số, ta được:
9x - 8x = 216
x = 216
Vậy quãng đường AB là 216 km.
Bài toán này là một ứng dụng thực tế của hàm số và phương trình bậc nhất. Việc giải bài toán này giúp học sinh hiểu rõ hơn về mối quan hệ giữa vận tốc, thời gian và quãng đường. Ngoài ra, bài toán còn rèn luyện kỹ năng giải phương trình và tư duy logic.
Để hiểu sâu hơn về các khái niệm liên quan đến hàm số và phương trình, học sinh có thể tham khảo thêm các bài học và bài tập khác trong sách giáo khoa và sách bài tập Toán 9 Kết nối tri thức tập 1.
Ngoài bài 5.25, sách bài tập Toán 9 Kết nối tri thức tập 1 còn có nhiều bài tập tương tự về hàm số và phương trình. Một số dạng bài tập thường gặp bao gồm:
Để làm tốt các bài tập này, học sinh cần nắm vững kiến thức lý thuyết và luyện tập thường xuyên.
Khi giải bài tập Toán 9, học sinh nên:
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài 5.25 trang 68 sách bài tập Toán 9 Kết nối tri thức tập 1 và các bài tập tương tự. Chúc các em học tốt!
Lưu ý: Bài giải trên chỉ mang tính chất tham khảo. Học sinh nên tự mình suy nghĩ và giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng.