Bài 4.36 trang 53 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.36 trang 53, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Tìm độ dài dây cáp mắc giữa hai cọc ở vị trí C, D trên hai bên bờ vực như trong Hình 4.21 (làm tròn đến mét).
Đề bài
Tìm độ dài dây cáp mắc giữa hai cọc ở vị trí C, D trên hai bên bờ vực như trong Hình 4.21 (làm tròn đến mét).
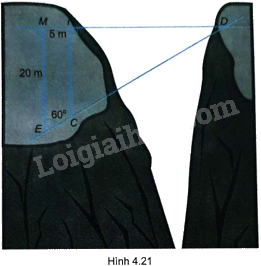
Phương pháp giải - Xem chi tiết
+ Theo kết quả bài 4.23: Cho hai điểm A, B. Nếu AN và PM cùng vuông góc MN, \(MN = n\), \(MP = p\), \(p > n\) và \(\widehat {MPA} = \alpha \) thì \(AB = \frac{{p\tan \alpha - n}}{{\sin \alpha }}\).
+ Thay \(p = 20m,n = 5m,\alpha = {60^o}\), \(\tan {60^o} = \sqrt 3 ;\sin {60^o} = \frac{{\sqrt 3 }}{2}\) ta có: \(CD = \frac{{20\sqrt 3 - 5}}{{\frac{{\sqrt 3 }}{2}}}\), từ đó tính được CD.
Lời giải chi tiết
Áp dụng bài tập 4.23 với \(p = 20m,n = 5m,\alpha = {60^o}\).
Do \(\tan {60^o} = \sqrt 3 ;\sin {60^o} = \frac{{\sqrt 3 }}{2}\)
suy ra \(CD = \frac{{20\sqrt 3 - 5}}{{\frac{{\sqrt 3 }}{2}}} \) \(= \frac{{2\left( {20\sqrt 3 - 5} \right)}}{{\sqrt 3 }} = \frac{{120 - 10\sqrt 3 }}{3} \approx 34\left( m \right)\)
Bài 4.36 trang 53 sách bài tập Toán 9 Kết nối tri thức tập 1 thuộc chương Hàm số bậc nhất và hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Đề bài cụ thể của bài 4.36 sẽ được trình bày đầy đủ tại đây. Ví dụ: Cho hàm số y = 2x + 1. Tìm giá trị của x khi y = 5.)
Lời giải:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta cùng xem xét một số ví dụ minh họa:
Ví dụ 1: (Đề bài ví dụ 1 và lời giải chi tiết)
Ví dụ 2: (Đề bài ví dụ 2 và lời giải chi tiết)
Ngoài ra, các em có thể tự giải các bài tập tương tự sau đây để rèn luyện kỹ năng:
Khi giải bài tập về hàm số, các em cần lưu ý những điều sau:
Bài 4.36 trang 53 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn khi giải các bài tập tương tự. Chúc các em học tốt!
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| y = ax2 + bx + c | Hàm số bậc hai |
| x = -b / 2a | Hoành độ đỉnh của parabol |