Bài 5.30 trang 71 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.30 trang 71, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác vuông ABC ((widehat A = {90^o})) có (widehat C = {30^o}) và AB=3cm. Đường phân giác của góc B cắt AC tại D. a) Chứng minh rằng đường tròn (D; DA) tiếp xúc với cạnh BC. b) Tính độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn tương ứng với cung ấy. c) Tính diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC).
Đề bài
Cho tam giác vuông ABC (\(\widehat A = {90^o}\)) có \(\widehat C = {30^o}\) và AB=3cm. Đường phân giác của góc B cắt AC tại D.
a) Chứng minh rằng đường tròn (D; DA) tiếp xúc với cạnh BC.
b) Tính độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn tương ứng với cung ấy.
c) Tính diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC).
Phương pháp giải - Xem chi tiết
a) + Qua D kẻ đường thẳng vuông góc với BC, cắt BC tại E.
+ Sử dụng tính chất tia phân giác của góc suy ra \(AD = DE\).
+ Do đó, đường tròn (D; DA) tiếp xúc với cạnh BC tại E.
b) + \(\widehat {ABC} = {90^o} - \widehat {BCA}\) nên \(\widehat {ABD} = \widehat {DBC} = \frac{1}{2}\widehat {ABC} = {30^o}\).
+ Tam giác ABD vuông tại A nên \(AD = AB.\tan \widehat {ABD}\).
+ \(\widehat {BDC} = {180^o} - \widehat {DBC} - \widehat {DCB}\) nên tính được số đo cung nằm trong góc BDC của đường tròn (D; DA).
+ Từ đó tính được độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn của cung nằm trong góc BDC của đường tròn (D; DA)
c) + Tam giác ABC vuông tại A nên \(AC = AB.\cot \widehat {ACB}\), từ đó tính được DC.
Diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC) là: \({S_{vk}} = \pi \left( {D{C^2} - D{A^2}} \right)\).
Lời giải chi tiết
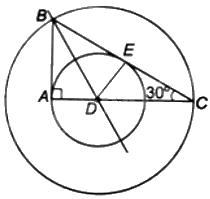
a) Qua D kẻ đường thẳng vuông góc với BC, cắt BC tại E.
Vì BD là phân giác của góc ABC, AD vuông góc với AB tại A, DE vuông góc với BC tại E nên \(AD = DE\). Do đó, đường tròn (D; DA) tiếp xúc với cạnh BC tại E.
b) Tam giác ABC vuông tại A nên
\(\widehat {ABC} = {90^o} - \widehat {BCA} = {60^o}\).
Vì BA là tia phân giác của góc ABC nên
\(\widehat {ABD} = \widehat {DBC} = \frac{1}{2}\widehat {ABC} = {30^o}\).
Tam giác ABD vuông tại A nên
\(AD = AB.\tan \widehat {ABD} = 3.\tan {30^o} = \sqrt 3 \left( {cm} \right)\).
Tam giác BDC có:
\(\widehat {BDC} = {180^o} - \widehat {DBC} - \widehat {DCB} = {120^o}\).
Do đó, cung nằm trong góc BDC của đường tròn (D; DA) có số đo bằng \({120^o}\).
Độ dài cung nằm trong góc BDC của đường tròn (D; DA) là:
\(l = \frac{{120}}{{180}}.\pi .\sqrt 3 = \frac{{2\sqrt 3 \pi }}{3}\left( {cm} \right)\).
Diện tích hình quạt tròn của cung nằm trong góc BDC của đường tròn (D; DA) là:
\(S = \frac{{120}}{{360}}.\pi .{\left( {\sqrt 3 } \right)^2} = \pi \left( {c{m^2}} \right)\)
c) Tam giác ABC vuông tại A nên
\(AC = AB.\cot \widehat {ACB} = 3.\cot {30^o} = 3\sqrt 3 \left( {cm} \right)\).
Do đó, \(DC = AC - AD = 2\sqrt 3 \left( {cm} \right)\)
Diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC) là:
\({S_{vk}} = \pi \left( {D{C^2} - D{A^2}} \right) \\= \pi \left[ {{{\left( {2\sqrt 3 } \right)}^2} - {{\left( {\sqrt 3 } \right)}^2}} \right] \\= 9\pi \left( {c{m^2}} \right)\)
Trước khi đi vào giải chi tiết bài 5.30, chúng ta cùng ôn lại một số kiến thức cơ bản về hàm số bậc nhất và hàm số bậc hai. Hàm số bậc nhất có dạng y = ax + b (a ≠ 0), trong đó a là hệ số góc và b là tung độ gốc. Hàm số bậc hai có dạng y = ax² + bx + c (a ≠ 0), trong đó a, b, c là các hệ số. Việc hiểu rõ các tính chất của hàm số, đặc biệt là đồ thị hàm số, là rất quan trọng để giải quyết các bài toán liên quan.
Đề bài 5.30 thường yêu cầu học sinh xác định hàm số, tìm các điểm thuộc đồ thị hàm số, hoặc giải các bài toán ứng dụng liên quan đến hàm số. Để giải bài tập này, cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, vận dụng các kiến thức đã học để xây dựng phương trình hoặc hệ phương trình phù hợp.
(Phần này sẽ chứa lời giải chi tiết cho bài 5.30, bao gồm các bước giải, giải thích rõ ràng và các ví dụ minh họa. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững phương pháp giải.)
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 5.30, chúng ta sẽ cùng xem xét một số ví dụ minh họa. Sau đó, chúng ta sẽ đưa ra một số bài tập tương tự để các em tự luyện tập và củng cố kiến thức.
Để giải nhanh bài 5.30, các em có thể áp dụng một số mẹo sau:
Khi giải bài 5.30, các em cần lưu ý một số điểm sau:
Bài 5.30 trang 71 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng, giúp các em học sinh củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ hiểu rõ phương pháp giải và tự tin làm bài tập. Chúc các em học tốt!