Bài 9.29 trang 56 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.29, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình vuông ABCD có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.8. Tính tổng diện tích của bốn hình viên phân được giới hạn bởi các cạnh hình vuông (phần tô đậm trong hình).
Đề bài
Cho hình vuông ABCD có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.8. Tính tổng diện tích của bốn hình viên phân được giới hạn bởi các cạnh hình vuông (phần tô đậm trong hình).
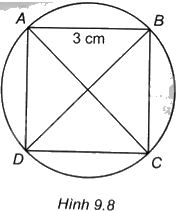
Phương pháp giải - Xem chi tiết
+ Tính diện tích hình vuông ABCD.
+ Áp dụng định lí Pythagore vào tam giác ABC vuông tại B tính được AC.
+ Đường tròn ngoại tiếp hình vuông ABCD có bán kính là: \(R = \frac{{AC}}{2}\).
+ Diện tích hình tròn ngoại tiếp hình vuông ABCD là: \({S_2} = \pi .{R^2}\).
Tổng diện tích bốn hình viên phân giới hạn bởi các cạnh hình vuông là: \(S = {S_2} - {S_1}\).
Lời giải chi tiết
Diện tích hình vuông ABCD là: \({S_1} = {3^2} = 9\left( {c{m^2}} \right)\).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có: \(A{C^2} = A{B^2} + B{C^2} = 18\) nên \(AC = 3\sqrt 2 cm\)
Đường tròn ngoại tiếp hình vuông ABCD có bán kính là: \(R = \frac{{AC}}{2} = \frac{{3\sqrt 2 }}{2}\left( {cm} \right)\).
Diện tích hình tròn ngoại tiếp hình vuông ABCD là: \({S_2} = \pi .{R^2} = \frac{9}{2}\pi \left( {c{m^2}} \right)\).
Tổng diện tích bốn hình viên phân giới hạn bởi các cạnh hình vuông là: \(S = {S_2} - {S_1} = \frac{9}{2}\pi - 9\left( {c{m^2}} \right)\).
Bài 9.29 thuộc chương Hàm số bậc nhất và hàm số bậc hai, sách bài tập Toán 9 - Kết nối tri thức tập 2. Bài toán này thường yêu cầu học sinh xác định hệ số góc, điểm đi qua, và vẽ đồ thị hàm số. Việc hiểu rõ các khái niệm này là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích đề bài để xác định rõ yêu cầu. Thông thường, bài 9.29 sẽ đưa ra một tình huống thực tế liên quan đến hàm số, yêu cầu học sinh xây dựng phương trình hàm số và giải các bài toán liên quan.
Phương pháp giải bài toán này bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 9.29. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một ví dụ minh họa:
Ví dụ: Một người nông dân có một mảnh đất hình chữ nhật. Chiều dài của mảnh đất hơn chiều rộng 5m. Nếu chiều dài tăng thêm 2m và chiều rộng giảm đi 1m thì diện tích mảnh đất tăng thêm 10m2. Tính chiều dài và chiều rộng ban đầu của mảnh đất.
Giải:
Ngoài bài 9.29, còn rất nhiều bài tập tương tự trong sách bài tập Toán 9 - Kết nối tri thức tập 2. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức về hàm số, phương trình, và hệ phương trình. Ngoài ra, việc luyện tập thường xuyên cũng rất quan trọng để rèn luyện kỹ năng giải toán.
Để học tốt môn Toán 9, đặc biệt là chương Hàm số bậc nhất và hàm số bậc hai, bạn có thể áp dụng một số mẹo sau:
Bài 9.29 trang 56 sách bài tập Toán 9 - Kết nối tri thức tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và các mẹo học tập trên, các em học sinh sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.