Bài 5.11 trang 62 sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và ứng dụng thực tế để giải quyết các vấn đề liên quan.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.11 trang 62, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình thoi ABCD có (widehat A = {75^o}) và (AB = 6cm). Vẽ đường tròn (D), bán kính 6cm. a) Chứng minh rằng A, C( in left( D right)). b) Tính độ dài cung nhỏ AC và diện tích hình quạt tròn ứng với cung nhỏ AC.
Đề bài
Cho hình thoi ABCD có \(\widehat A = {75^o}\) và \(AB = 6cm\). Vẽ đường tròn (D), bán kính 6cm.
a) Chứng minh rằng A, C \( \in \left( D \right)\).
b) Tính độ dài cung nhỏ AC và diện tích hình quạt tròn ứng với cung nhỏ AC.
Phương pháp giải - Xem chi tiết
Độ dài l của cung \({n^o}\) trên đường tròn (O; R) là \(l = \frac{n}{{180}}.\pi R\).
Diện tích \({S_q}\) của hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{n}{{360}}.\pi {R^2}\).
Lời giải chi tiết
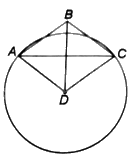
a) Vì ABCD là hình thoi nên \(AD = DC = 6cm\) (cùng bằng AB). Do đó, A, C \( \in \left( D; 6cm \right)\).
b) Vì ABCD là hình thoi nên \(\widehat {BAD} = \widehat {BCD} = {75^o},\widehat {ADC} = \widehat {ABC}\).
Lại có: \(\widehat {BAD} + \widehat {BCD} + \widehat {ADC} + \widehat {ABC} = {360^o}\),
suy ra \(2\widehat {ADC} = {360^o} - {2.75^o} = {210^o}\)
nên \(\widehat {ADC} = {105^o}\)
Góc ADC là góc ở tâm chắn cung nhỏ AC nên sđ$\overset\frown{AC}$nhỏ \( = \widehat {ADC} = {105^o}\).
Độ dài cung nhỏ AC là:
${{l}_{\overset\frown{AC}}}=\frac{105}{180}.\pi .6=\frac{7\pi }{2}\left( cm \right)$
Diện tích hình quạt tròn ứng với cung nhỏ AC là:
${{S}_{\overset\frown{AC}}}=\frac{105}{360}.\pi {{.6}^{2}}=\frac{21\pi }{2}\left( c{{m}^{2}} \right)$.
Trước khi đi vào giải chi tiết bài 5.11, chúng ta cùng ôn lại một số kiến thức cơ bản về hàm số bậc nhất và cách xác định hàm số khi biết đồ thị. Hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc. Đồ thị của hàm số bậc nhất là một đường thẳng.
Để xác định hàm số khi biết đồ thị, ta cần tìm hai điểm thuộc đồ thị và thay tọa độ của hai điểm này vào phương trình y = ax + b để tìm a và b.
Đề bài: (Sách bài tập Toán 9 - Kết nối tri thức tập 1)
Cho hàm số y = ax + b. Biết rằng đồ thị của hàm số đi qua hai điểm A(0; -2) và B(1; 1).
a) Xác định hệ số a và b.
b) Vẽ đồ thị của hàm số.
c) Tính giá trị của y khi x = -2.
a) Xác định hệ số a và b:
Vì đồ thị của hàm số y = ax + b đi qua điểm A(0; -2), ta có:
-2 = a * 0 + b => b = -2
Vì đồ thị của hàm số y = ax + b đi qua điểm B(1; 1), ta có:
1 = a * 1 + b => 1 = a - 2 => a = 3
Vậy, hàm số có dạng y = 3x - 2.
Để vẽ đồ thị của hàm số y = 3x - 2, ta cần xác định hai điểm thuộc đồ thị. Ta đã có hai điểm A(0; -2) và B(1; 1). Vẽ đường thẳng đi qua hai điểm này, ta được đồ thị của hàm số.
Thay x = -2 vào hàm số y = 3x - 2, ta được:
y = 3 * (-2) - 2 = -6 - 2 = -8
Vậy, khi x = -2 thì y = -8.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập tương tự sau:
Ngoài ra, các em có thể tìm hiểu thêm về các ứng dụng của hàm số bậc nhất trong thực tế, ví dụ như tính quãng đường đi được của một vật chuyển động đều, tính tiền điện tiêu thụ hàng tháng,...
Bài 5.11 trang 62 Sách bài tập Toán 9 - Kết nối tri thức tập 1 là một bài tập cơ bản nhưng quan trọng trong chương trình học. Việc nắm vững kiến thức về hàm số bậc nhất và phương pháp giải bài tập này sẽ giúp các em học tốt môn Toán 9 và chuẩn bị cho các kỳ thi sắp tới.