Bài 2.19 trang 28 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và ứng dụng thực tế của nó.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.19 trang 28, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin giải các bài tập tương tự.
Chiều dài của một hình chữ nhật thì luôn lớn hơn hoặc bằng chiều rộng. Hãy viết và giải bất phương trình để tìm giá trị có thể của x (cm) trong hình vẽ dưới đây:
Đề bài
Chiều dài của một hình chữ nhật thì luôn lớn hơn hoặc bằng chiều rộng. Hãy viết và giải bất phương trình để tìm giá trị có thể của x (cm) trong hình vẽ dưới đây:
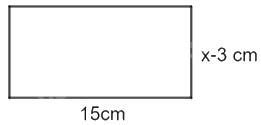
Phương pháp giải - Xem chi tiết
+ Vì chiều dài của một hình chữ nhật thì luôn lớn hơn hoặc bằng chiều rộng nên \(x - 3 \le 15\)
+ Giải bất phương trình đó.
+ Vì chiều dài, chiều rộng hình chữ nhật luôn lớn hơn 0 nên \(x - 3 > 0\) hay \(x > 3\).
+ Kết hợp các điều kiện lại, ta tìm được khoảng giá trị của x.
Lời giải chi tiết
Vì chiều dài của một hình chữ nhật thì luôn lớn hơn hoặc bằng chiều rộng nên \(x - 3 \le 15\) nên \(x \le 18\).
Mà \(x - 3 > 0\) (do chiều rộng của hình chữ nhật lớn hơn 0) hay \(x > 3\).
Vậy giá trị có thể nhận là \(3 < x \le 18\).
Bài 2.19 trang 28 sách bài tập Toán 9 Kết nối tri thức tập 1 yêu cầu chúng ta giải quyết một bài toán thực tế liên quan đến hàm số bậc nhất. Bài toán thường mô tả một tình huống cụ thể, ví dụ như sự thay đổi của một đại lượng theo thời gian hoặc theo một đại lượng khác. Để giải bài toán này, chúng ta cần xác định được hàm số bậc nhất mô tả mối quan hệ giữa các đại lượng và sử dụng các tính chất của hàm số để tìm ra kết quả.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp chúng ta tránh được những sai sót không đáng có và tìm ra hướng giải quyết phù hợp. Hãy chú ý đến các thông tin quan trọng được cung cấp trong đề bài, chẳng hạn như các giá trị đã biết, các đại lượng cần tìm và mối quan hệ giữa chúng.
Sau khi đã hiểu rõ đề bài, chúng ta cần xây dựng một mô hình toán học để mô tả bài toán. Mô hình này thường bao gồm việc xác định các biến số, các hệ số và các phương trình liên quan. Trong trường hợp của bài 2.19, chúng ta cần xác định hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các hệ số cần tìm.
Khi đã có mô hình toán học, chúng ta có thể giải các phương trình để tìm ra các giá trị của các biến số. Trong trường hợp của bài 2.19, chúng ta có thể sử dụng các thông tin được cung cấp trong đề bài để lập hệ phương trình và giải hệ phương trình đó để tìm ra các giá trị của a và b. Sau khi đã tìm được các giá trị của a và b, chúng ta có thể viết được phương trình hàm số bậc nhất mô tả mối quan hệ giữa các đại lượng.
Sau khi đã tìm được kết quả, chúng ta cần kiểm tra lại kết quả đó để đảm bảo rằng nó là chính xác và phù hợp với thực tế. Chúng ta có thể thay các giá trị đã tìm được vào phương trình hàm số và kiểm tra xem phương trình đó có thỏa mãn các điều kiện của đề bài hay không. Nếu kết quả không thỏa mãn các điều kiện của đề bài, chúng ta cần xem lại các bước giải và tìm ra những sai sót.
Giả sử đề bài yêu cầu chúng ta tìm hàm số bậc nhất đi qua hai điểm A(1; 2) và B(3; 6). Chúng ta có thể làm như sau:
Ngoài bài 2.19, còn rất nhiều bài tập tương tự yêu cầu chúng ta vận dụng kiến thức về hàm số bậc nhất. Các bài tập này có thể yêu cầu chúng ta tìm hệ số của hàm số, xác định điểm thuộc đồ thị hàm số, hoặc giải các bài toán thực tế liên quan đến hàm số. Để giải các bài tập này, chúng ta cần nắm vững các khái niệm và tính chất của hàm số bậc nhất và luyện tập thường xuyên.
Bài 2.19 trang 28 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng giúp chúng ta hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Bằng cách phân tích đề bài, xây dựng mô hình toán học, giải phương trình và kiểm tra lại kết quả, chúng ta có thể tự tin giải quyết bài toán này và các bài tập tương tự.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 2.19 trang 28 sách bài tập Toán 9 Kết nối tri thức tập 1. Chúc các em học tập tốt!