Giải bài 5.5 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1

Bài 5.5 trang 56 sách bài tập Toán 9 Kết nối tri thức tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai. Bài tập này thường yêu cầu học sinh áp dụng các công thức và phương pháp đã học để tìm ra nghiệm của phương trình.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.5 trang 56, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho đường tròn (O), đường kính AB và điểm M thuộc (O) (M không trùng với điểm nào trong hai điểm A và B). Trên (O) lấy điểm N nằm khác phía của M đối với đường thẳng AB sao cho (AM = BN). Chứng minh rằng O là trung điểm của đoạn MN.

Đề bài

Cho đường tròn (O), đường kính AB và điểm M thuộc (O) (M không trùng với điểm nào trong hai điểm A và B). Trên (O) lấy điểm N nằm khác phía của M đối với đường thẳng AB sao cho \(AM = BN\). Chứng minh rằng O là trung điểm của đoạn MN.

Phương pháp giải - Xem chi tiết Giải bài 5.5 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1 1

+ Chứng minh \(\Delta AOM = \Delta BON\left( {c.c.c} \right)\), suy ra \(\widehat {MAO} = \widehat {NBO}\), từ đó chứng minh được AM//BN.

+ Chứng minh tứ giác AMBN là hình bình hành, suy ra O là trung điểm của đoạn MN.

Lời giải chi tiết

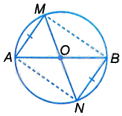
Giải bài 5.5 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1 2

Tam giác AOM và tam giác BON có: \(OA = OB,OM = ON,AM = BN\) nên \(\Delta AOM = \Delta BON\left( {c.c.c} \right)\).

Suy ra \(\widehat {MAO} = \widehat {NBO}\), mà hai góc này ở vị trí so le trong nên AM//BN.

Tứ giác AMBN có: AM//BN, \(AM = BN\) nên AMBN là hình bình hành.

Mà O là trung điểm của AB nên O là trung điểm của đoạn MN.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 5.5 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1 đặc sắc thuộc chuyên mục bài tập toán 9 trên nền tảng toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 5.5 trang 56 sách bài tập Toán 9 - Kết nối tri thức tập 1: Hướng dẫn chi tiết

Bài 5.5 trang 56 sách bài tập Toán 9 Kết nối tri thức tập 1 yêu cầu giải phương trình bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức về phương trình bậc hai, bao gồm:

Dạng tổng quát của phương trình bậc hai: ax² + bx + c = 0 (a ≠ 0)
Công thức nghiệm tổng quát: x = (-b ± √(b² - 4ac)) / 2a
Định lý về dấu của nghiệm:
- Nếu Δ > 0: Phương trình có hai nghiệm phân biệt
- Nếu Δ = 0: Phương trình có nghiệm kép
- Nếu Δ < 0: Phương trình vô nghiệm

Lời giải chi tiết bài 5.5 trang 56

Để giải bài 5.5 trang 56, chúng ta cần xác định các hệ số a, b, c của phương trình. Sau đó, tính delta (Δ) và dựa vào giá trị của delta để xác định số nghiệm và tính nghiệm của phương trình.

Ví dụ: Giả sử phương trình cần giải là 2x² - 5x + 2 = 0

Xác định hệ số: a = 2, b = -5, c = 2
Tính delta: Δ = b² - 4ac = (-5)² - 4 * 2 * 2 = 25 - 16 = 9
Xác định số nghiệm: Vì Δ > 0, phương trình có hai nghiệm phân biệt
Tính nghiệm:
- x₁ = (-b + √Δ) / 2a = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
- x₂ = (-b - √Δ) / 2a = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 0.5

Vậy, nghiệm của phương trình 2x² - 5x + 2 = 0 là x₁ = 2 và x₂ = 0.5

Các dạng bài tập tương tự và phương pháp giải

Ngoài bài 5.5 trang 56, sách bài tập Toán 9 Kết nối tri thức tập 1 còn nhiều bài tập tương tự về phương trình bậc hai. Để giải các bài tập này, bạn cần:

Nắm vững các công thức và định lý liên quan đến phương trình bậc hai.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Kiểm tra lại kết quả sau khi giải để đảm bảo tính chính xác.

Mẹo giải nhanh

Trong một số trường hợp, bạn có thể sử dụng các mẹo sau để giải nhanh phương trình bậc hai:

Sử dụng công thức nghiệm thu gọn: Nếu b là số chẵn, bạn có thể sử dụng công thức nghiệm thu gọn để tính nghiệm nhanh hơn.
Phân tích đa thức thành nhân tử: Nếu phương trình có thể phân tích thành nhân tử, bạn có thể tìm nghiệm bằng cách giải các phương trình bậc nhất tương ứng.

Lưu ý quan trọng

Khi giải phương trình bậc hai, bạn cần chú ý đến các điều kiện sau:

Kiểm tra xem phương trình có phải là phương trình bậc hai hay không.
Xác định đúng các hệ số a, b, c của phương trình.
Tính toán cẩn thận để tránh sai sót.

Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 5.5 trang 56 sách bài tập Toán 9 Kết nối tri thức tập 1 và các bài tập tương tự. Chúc các em học tốt!