Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu bộ câu hỏi trắc nghiệm trang 18, 19 sách bài tập Toán 9 - Kết nối tri thức tập 2, được giải chi tiết và dễ hiểu.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và tự tin hơn trong các kỳ thi. Hãy cùng chúng tôi khám phá lời giải chi tiết cho từng câu hỏi nhé!
Hình vẽ dưới đây là đồ thị của hàm số nào? A. (y = {x^2}). B. (y = - frac{1}{2}{x^2}). C. (y = frac{1}{4}{x^2}). D. (y = frac{1}{3}{x^2}).
Trả lời câu hỏi Câu 2 trang 18 SBT Toán 9 Kết nối tri thức
Cho hàm số \(y = - \frac{2}{5}{x^2}\) có đồ thị là parabol (P). Điểm trên (P) khác gốc tọa độ O (0; 0) có tung độ gấp ba lần hoành độ thì có hoành độ là
A. \( - \frac{{15}}{2}\).
B. \(\frac{{15}}{2}\).
C. \(\frac{2}{{15}}\).
D. \( - \frac{2}{{15}}\).
Phương pháp giải:
+ Gọi tọa độ của điểm cần tìm là B(x; 3x) (với \(x \ne 0\)).
+ Vì B thuộc parabol (P) nên ta có: \(3x = - \frac{2}{5}{x^2}\).
+ Giải phương trình thu được tìm được x.
Lời giải chi tiết:
Gọi tọa độ của điểm cần tìm là B (x; 3x) (với \(x \ne 0\)). Vì B thuộc parabol (P) nên ta có: \(3x = - \frac{2}{5}{x^2}\)
\(\frac{2}{5}{x^2} + 3x = 0\)
\(x\left( {\frac{2}{5}x + 3} \right) = 0\)
\(x = 0\) (loại) hoặc \(\frac{2}{5}x + 3 = 0\)
\(x = \frac{{ - 15}}{2}\)
Vậy điểm thỏa mãn yêu cầu bài toán có hoành độ là \( - \frac{{15}}{2}\).
Chọn A
Trả lời câu hỏi Câu 3 trang 18 SBT Toán 9 Kết nối tri thức
Trong các điểm A(1; -2), B(-1; -1), C(10; -200), \(D\left( {\sqrt {10} ; - 20} \right)\), có bao nhiêu điểm thuộc đồ thị của hàm số \(y = - 2{x^2}\)?
A. 2.
B. 1.
C. 3.
D. 4.
Phương pháp giải:
Thay tọa độ từng điểm vào hàm số \(y = - 2{x^2}\), nếu đẳng thức thu được đúng thì điểm đó thuộc đồ thị hàm số.
Lời giải chi tiết:
Thay \(x = 1;y = - 2\) vào \(y = - 2{x^2}\) ta có: \( - 2 = - {2.1^2}\) (luôn đúng) nên điểm A(1; -2) thuộc đồ thị hàm số \(y = - 2{x^2}\).
Thay \(x = - 1;y = - 1\) vào \(y = - 2{x^2}\) ta có: \( - 1 = - 2.{\left( { - 1} \right)^2}\) (vô lí) nên điểm B(-1; -1) không thuộc đồ thị hàm số \(y = - 2{x^2}\).
Thay \(x = 10;y = - 200\) vào \(y = - 2{x^2}\) ta có: \( - 200 = - {2.10^2}\) (luôn đúng) nên điểm C(10; -200) thuộc đồ thị hàm số \(y = - 2{x^2}\).
Thay \(x = \sqrt {10} ;y = - 20\) vào \(y = - 2{x^2}\) ta có: \( - 20 = - 2.{\left( {\sqrt {10} } \right)^2}\) (luôn đúng) nên điểm \(D\left( {\sqrt {10} ; - 20} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
Vậy ba điểm A(1; -2), C(10; -200), \(D\left( {\sqrt {10} ; - 20} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
Chọn C
Trả lời câu hỏi Câu 4 trang 19 SBT Toán 9 Kết nối tri thức
Tọa độ một giao điểm của parabol (P): \(y = \frac{1}{2}{x^2}\) và đường thẳng (d): \(y = x + \frac{3}{2}\) là
A. \(\left( {1;\frac{1}{2}} \right)\).
B. \(\left( {\frac{1}{2};2} \right)\).
C. \(\left( { - \frac{1}{2};1} \right)\).
D. \(\left( { - 1;\frac{1}{2}} \right)\).
Phương pháp giải:
+ Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình: \(\frac{1}{2}{x^2} = x + \frac{3}{2}\).
+ Giải phương trình thu được tìm được x.
+ Thay x tìm được vào \(y = x + \frac{3}{2}\), từ đó tìm được tọa độ giao điểm của d và (P).
Lời giải chi tiết:
Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình: \(\frac{1}{2}{x^2} = x + \frac{3}{2}\), suy ra \({x^2} - 2x - 3 = 0\).
Vì \(1 + 2 - 3 = 0\) nên phương trình \({x^2} - 2x - 3 = 0\) có hai nghiệm \({x_1} = - 1;{x_2} = \frac{3}{1} = 3\).
Với \(x = - 1\) thay vào \(y = x + \frac{3}{2}\) ta có: \(y = - 1 + \frac{3}{2} = \frac{1}{2}\).
Với \(x = 3\) thay vào \(y = x + \frac{3}{2}\) ta có: \(y = 3 + \frac{3}{2} = \frac{9}{2}\).
Do đó, tọa độ một giao điểm của parabol (P): \(y = \frac{1}{2}{x^2}\) và đường thẳng (d): \(y = x + \frac{3}{2}\) là \(\left( { - 1;\frac{1}{2}} \right)\).
Chọn D
Trả lời câu hỏi Câu 5 trang 19 SBT Toán 9 Kết nối tri thức
Để điểm \(A\left( { - \frac{{\sqrt 2 }}{{\sqrt 5 }};m\sqrt 5 } \right)\) nằm trên parabol \(y = - \sqrt 5 {x^2}\) thì giá trị của m bằng
A. \(m = - \frac{5}{2}\).
B. \(m = \frac{2}{5}\).
C. \(m = - \frac{2}{5}\).
D. \(m = \frac{5}{2}\).
Phương pháp giải:
Thay \(x = - \frac{{\sqrt 2 }}{{\sqrt 5 }};y = m\sqrt 5 \) vào \(y = - \sqrt 5 {x^2}\), thu được phương trình ẩn m, giải phương trình đó để tìm m.
Lời giải chi tiết:
Để điểm A nằm trên parabol thì: \(m\sqrt 5 = - \sqrt 5 .{\left( {\frac{{ - \sqrt 2 }}{{\sqrt 5 }}} \right)^2} = \frac{{ - 2}}{{\sqrt 5 }}\), suy ra \(m = \frac{{ - 2}}{{\sqrt 5 }}:\sqrt 5 = \frac{{ - 2}}{5}\).
Chọn C
Trả lời câu hỏi Câu 7 trang 19 SBT Toán 9 Kết nối tri thức
Không giải phương trình, hãy tính tổng hai nghiệm của phương trình \( - 3{x^2} + 5x + 1 = 0\).
A. \( - \frac{5}{6}\).
B. \(\frac{5}{3}\).
C. \( - \frac{5}{3}\).
D. \(\frac{5}{6}\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Nếu \(\Delta > 0\) thì áp dụng định lí Viète để tính tổng các nghiệm \({x_1} + {x_2} = \frac{{ - b}}{a}\).
Lời giải chi tiết:
Vì \(\Delta = {5^2} - 4.\left( { - 3} \right).1 = 37 > 0\) nên phương trình có hai nghiệm. Theo định lí Viète ta có tổng hai nghiệm của phương trình là: \(\frac{{ - 5}}{{ - 3}} = \frac{5}{3}\)
Chọn B
Trả lời câu hỏi Câu 6 trang 19 SBT Toán 9 Kết nối tri thức
Cho parabol (P): \(y = \left( {m - \frac{3}{4}} \right){x^2}\), với \(m \ne \frac{3}{4}\) và đường thẳng \(y = 3x - 5\). Biết đường thẳng d cắt (P) tại một điểm có tung độ \(y = 1\). Tìm m và hoành độ giao điểm còn lại của d và (P).
A. \(m = 0;x = 2\).
B. \(m = 1;x = 2\).
C. \(m = 1;x = 10\).
D. \(m = \frac{5}{4};x = 10\).
Phương pháp giải:
+ Gọi D là giao điểm của d và (P).
+ Vì d cắt (P) tại một điểm có tung độ \(y = 1\) nên ta có: \(1 = 3.x - 5\), từ đó tìm được x và tìm được tọa độ của D.
+ Thay tọa độ điểm D vào \(y = \left( {m - \frac{3}{4}} \right){x^2}\), thu được phương trình ẩn m, giải phương trình tìm được m.
Lời giải chi tiết:
Gọi D là giao điểm của d và (P). Vì đường thẳng d cắt (P) tại một điểm có tung độ \(y = 1\) nên ta có: \(1 = 3.x - 5\), suy ra \(x = 2\). Do đó, D(2; 1).
Vì D(2; 1) thuộc (P) nên ta có: \(1 = \left( {m - \frac{3}{4}} \right){.2^2}\), suy ra \(4m - 3 = 1\), suy ra \(m = 1\).
Chọn B
Trả lời câu hỏi Câu 8 trang 19 SBT Toán 9 Kết nối tri thức
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \( - {x^2} - 4x + 6 = 0\). Không giải phương trình, tính giá trị của biểu thức \(M = \frac{1}{{{x_1} + 2}} + \frac{1}{{{x_2} + 2}}\).
A. \(M = 0\).
B. \(M = 1\).
C. \(M = 4\).
D. \(M = - 2\).
Phương pháp giải:
+ Viết định lí Viète để tính tổng và tích các nghiệm \({x_1} + {x_2};{x_1}.{x_2}\).
+ Biến đổi \(M = \frac{{{x_2} + 2 + {x_1} + 2}}{{\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right)}} = \frac{{\left( {{x_1} + {x_2}} \right) + 4}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\), với \({x_1} + {x_2};{x_1}.{x_2}\) đã tính ở trên, ta tính M.
Lời giải chi tiết:
Ta có: \(M = \frac{{{x_2} + 2 + {x_1} + 2}}{{\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right)}} = \frac{{\left( {{x_1} + {x_2}} \right) + 4}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\)
Theo định lí Viète ta có: \({x_1} + {x_2} = \frac{{ - \left( { - 4} \right)}}{{ - 1}} = - 4;{x_1}.{x_2} = \frac{6}{{ - 1}} = - 6\). Do đó, \(M = \frac{{ - 4 + 4}}{{ - 6 + 2.\left( { - 4} \right) + 4}} = 0\).
Chọn A
Trả lời câu hỏi Câu 9 trang 19 SBT Toán 9 Kết nối tri thức
Tìm điều kiện của tham số m để phương trình \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 3m + 5 = 0\) có hai nghiệm phân biệt.
A. \(m \le - 1\).
B. \(m = - 1\).
C. \(m > - 1\).
D. \(m < - 1\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt.
Lời giải chi tiết:
Phương trình đã cho có hai nghiệm phân biệt khi \(\Delta ' > 0\) nên \({\left[ { - \left( {m - 2} \right)} \right]^2} - 1.\left( {{m^2} - 3m + 5} \right) > 0\)
\({m^2} - 4m + 4 - {m^2} + 3m - 5 > 0\)
\( - m - 1 > 0\)
\(m < - 1\)
Chọn D
Trả lời câu hỏi Câu 10 trang 19 SBT Toán 9 Kết nối tri thức
Nếu hai số u, v có tổng là 7 và tích là -8 thì chúng là hai nghiệm của phương trình nào?
A. \({x^2} + 7x - 8 = 0\).
B. \({x^2} - 7x - 8 = 0\).
C. \({x^2} + 7x + 8 = 0\).
D. \({x^2} - 7x + 8 = 0\).
Phương pháp giải:
Hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình \({x^2} - Sx + P = 0\) (điều kiện \({S^2} - 4P \ge 0\)).
Lời giải chi tiết:
Nếu hai số u và v có tổng là 7 và tích là -8 thì chúng là hai nghiệm của phương trình \({x^2} - 7x - 8 = 0\)
Chọn B
Trả lời câu hỏi Câu 1 trang 18 SBT Toán 9 Kết nối tri thức
Hình vẽ dưới đây là đồ thị của hàm số nào?
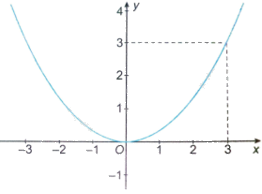
A. \(y = {x^2}\).
B. \(y = - \frac{1}{2}{x^2}\).
C. \(y = \frac{1}{4}{x^2}\).
D. \(y = \frac{1}{3}{x^2}\).
Phương pháp giải:
Nhận thấy điểm (3; 3) vừa thuộc đồ thị hàm số trong hình vẽ, vừa thuộc hàm số \(y = \frac{1}{3}{x^2}\) nên đồ thị hàm số trong hình vẽ là \(y = \frac{1}{3}{x^2}\).
Lời giải chi tiết:
Đồ thị hàm trong hình vẽ đi qua điểm (3; 3). Trong các hàm số trên, điểm (3; 3) chỉ thuộc hàm số \(y = \frac{1}{3}{x^2}\) nên hình vẽ là đồ thị của hàm số \(y = \frac{1}{3}{x^2}\).
Chọn D
Trả lời câu hỏi Câu 1 trang 18 SBT Toán 9 Kết nối tri thức
Hình vẽ dưới đây là đồ thị của hàm số nào?
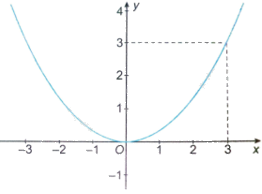
A. \(y = {x^2}\).
B. \(y = - \frac{1}{2}{x^2}\).
C. \(y = \frac{1}{4}{x^2}\).
D. \(y = \frac{1}{3}{x^2}\).
Phương pháp giải:
Nhận thấy điểm (3; 3) vừa thuộc đồ thị hàm số trong hình vẽ, vừa thuộc hàm số \(y = \frac{1}{3}{x^2}\) nên đồ thị hàm số trong hình vẽ là \(y = \frac{1}{3}{x^2}\).
Lời giải chi tiết:
Đồ thị hàm trong hình vẽ đi qua điểm (3; 3). Trong các hàm số trên, điểm (3; 3) chỉ thuộc hàm số \(y = \frac{1}{3}{x^2}\) nên hình vẽ là đồ thị của hàm số \(y = \frac{1}{3}{x^2}\).
Chọn D
Trả lời câu hỏi Câu 2 trang 18 SBT Toán 9 Kết nối tri thức
Cho hàm số \(y = - \frac{2}{5}{x^2}\) có đồ thị là parabol (P). Điểm trên (P) khác gốc tọa độ O (0; 0) có tung độ gấp ba lần hoành độ thì có hoành độ là
A. \( - \frac{{15}}{2}\).
B. \(\frac{{15}}{2}\).
C. \(\frac{2}{{15}}\).
D. \( - \frac{2}{{15}}\).
Phương pháp giải:
+ Gọi tọa độ của điểm cần tìm là B(x; 3x) (với \(x \ne 0\)).
+ Vì B thuộc parabol (P) nên ta có: \(3x = - \frac{2}{5}{x^2}\).
+ Giải phương trình thu được tìm được x.
Lời giải chi tiết:
Gọi tọa độ của điểm cần tìm là B (x; 3x) (với \(x \ne 0\)). Vì B thuộc parabol (P) nên ta có: \(3x = - \frac{2}{5}{x^2}\)
\(\frac{2}{5}{x^2} + 3x = 0\)
\(x\left( {\frac{2}{5}x + 3} \right) = 0\)
\(x = 0\) (loại) hoặc \(\frac{2}{5}x + 3 = 0\)
\(x = \frac{{ - 15}}{2}\)
Vậy điểm thỏa mãn yêu cầu bài toán có hoành độ là \( - \frac{{15}}{2}\).
Chọn A
Trả lời câu hỏi Câu 3 trang 18 SBT Toán 9 Kết nối tri thức
Trong các điểm A(1; -2), B(-1; -1), C(10; -200), \(D\left( {\sqrt {10} ; - 20} \right)\), có bao nhiêu điểm thuộc đồ thị của hàm số \(y = - 2{x^2}\)?
A. 2.
B. 1.
C. 3.
D. 4.
Phương pháp giải:
Thay tọa độ từng điểm vào hàm số \(y = - 2{x^2}\), nếu đẳng thức thu được đúng thì điểm đó thuộc đồ thị hàm số.
Lời giải chi tiết:
Thay \(x = 1;y = - 2\) vào \(y = - 2{x^2}\) ta có: \( - 2 = - {2.1^2}\) (luôn đúng) nên điểm A(1; -2) thuộc đồ thị hàm số \(y = - 2{x^2}\).
Thay \(x = - 1;y = - 1\) vào \(y = - 2{x^2}\) ta có: \( - 1 = - 2.{\left( { - 1} \right)^2}\) (vô lí) nên điểm B(-1; -1) không thuộc đồ thị hàm số \(y = - 2{x^2}\).
Thay \(x = 10;y = - 200\) vào \(y = - 2{x^2}\) ta có: \( - 200 = - {2.10^2}\) (luôn đúng) nên điểm C(10; -200) thuộc đồ thị hàm số \(y = - 2{x^2}\).
Thay \(x = \sqrt {10} ;y = - 20\) vào \(y = - 2{x^2}\) ta có: \( - 20 = - 2.{\left( {\sqrt {10} } \right)^2}\) (luôn đúng) nên điểm \(D\left( {\sqrt {10} ; - 20} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
Vậy ba điểm A(1; -2), C(10; -200), \(D\left( {\sqrt {10} ; - 20} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
Chọn C
Trả lời câu hỏi Câu 4 trang 19 SBT Toán 9 Kết nối tri thức
Tọa độ một giao điểm của parabol (P): \(y = \frac{1}{2}{x^2}\) và đường thẳng (d): \(y = x + \frac{3}{2}\) là
A. \(\left( {1;\frac{1}{2}} \right)\).
B. \(\left( {\frac{1}{2};2} \right)\).
C. \(\left( { - \frac{1}{2};1} \right)\).
D. \(\left( { - 1;\frac{1}{2}} \right)\).
Phương pháp giải:
+ Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình: \(\frac{1}{2}{x^2} = x + \frac{3}{2}\).
+ Giải phương trình thu được tìm được x.
+ Thay x tìm được vào \(y = x + \frac{3}{2}\), từ đó tìm được tọa độ giao điểm của d và (P).
Lời giải chi tiết:
Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình: \(\frac{1}{2}{x^2} = x + \frac{3}{2}\), suy ra \({x^2} - 2x - 3 = 0\).
Vì \(1 + 2 - 3 = 0\) nên phương trình \({x^2} - 2x - 3 = 0\) có hai nghiệm \({x_1} = - 1;{x_2} = \frac{3}{1} = 3\).
Với \(x = - 1\) thay vào \(y = x + \frac{3}{2}\) ta có: \(y = - 1 + \frac{3}{2} = \frac{1}{2}\).
Với \(x = 3\) thay vào \(y = x + \frac{3}{2}\) ta có: \(y = 3 + \frac{3}{2} = \frac{9}{2}\).
Do đó, tọa độ một giao điểm của parabol (P): \(y = \frac{1}{2}{x^2}\) và đường thẳng (d): \(y = x + \frac{3}{2}\) là \(\left( { - 1;\frac{1}{2}} \right)\).
Chọn D
Trả lời câu hỏi Câu 5 trang 19 SBT Toán 9 Kết nối tri thức
Để điểm \(A\left( { - \frac{{\sqrt 2 }}{{\sqrt 5 }};m\sqrt 5 } \right)\) nằm trên parabol \(y = - \sqrt 5 {x^2}\) thì giá trị của m bằng
A. \(m = - \frac{5}{2}\).
B. \(m = \frac{2}{5}\).
C. \(m = - \frac{2}{5}\).
D. \(m = \frac{5}{2}\).
Phương pháp giải:
Thay \(x = - \frac{{\sqrt 2 }}{{\sqrt 5 }};y = m\sqrt 5 \) vào \(y = - \sqrt 5 {x^2}\), thu được phương trình ẩn m, giải phương trình đó để tìm m.
Lời giải chi tiết:
Để điểm A nằm trên parabol thì: \(m\sqrt 5 = - \sqrt 5 .{\left( {\frac{{ - \sqrt 2 }}{{\sqrt 5 }}} \right)^2} = \frac{{ - 2}}{{\sqrt 5 }}\), suy ra \(m = \frac{{ - 2}}{{\sqrt 5 }}:\sqrt 5 = \frac{{ - 2}}{5}\).
Chọn C
Trả lời câu hỏi Câu 6 trang 19 SBT Toán 9 Kết nối tri thức
Cho parabol (P): \(y = \left( {m - \frac{3}{4}} \right){x^2}\), với \(m \ne \frac{3}{4}\) và đường thẳng \(y = 3x - 5\). Biết đường thẳng d cắt (P) tại một điểm có tung độ \(y = 1\). Tìm m và hoành độ giao điểm còn lại của d và (P).
A. \(m = 0;x = 2\).
B. \(m = 1;x = 2\).
C. \(m = 1;x = 10\).
D. \(m = \frac{5}{4};x = 10\).
Phương pháp giải:
+ Gọi D là giao điểm của d và (P).
+ Vì d cắt (P) tại một điểm có tung độ \(y = 1\) nên ta có: \(1 = 3.x - 5\), từ đó tìm được x và tìm được tọa độ của D.
+ Thay tọa độ điểm D vào \(y = \left( {m - \frac{3}{4}} \right){x^2}\), thu được phương trình ẩn m, giải phương trình tìm được m.
Lời giải chi tiết:
Gọi D là giao điểm của d và (P). Vì đường thẳng d cắt (P) tại một điểm có tung độ \(y = 1\) nên ta có: \(1 = 3.x - 5\), suy ra \(x = 2\). Do đó, D(2; 1).
Vì D(2; 1) thuộc (P) nên ta có: \(1 = \left( {m - \frac{3}{4}} \right){.2^2}\), suy ra \(4m - 3 = 1\), suy ra \(m = 1\).
Chọn B
Trả lời câu hỏi Câu 7 trang 19 SBT Toán 9 Kết nối tri thức
Không giải phương trình, hãy tính tổng hai nghiệm của phương trình \( - 3{x^2} + 5x + 1 = 0\).
A. \( - \frac{5}{6}\).
B. \(\frac{5}{3}\).
C. \( - \frac{5}{3}\).
D. \(\frac{5}{6}\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Nếu \(\Delta > 0\) thì áp dụng định lí Viète để tính tổng các nghiệm \({x_1} + {x_2} = \frac{{ - b}}{a}\).
Lời giải chi tiết:
Vì \(\Delta = {5^2} - 4.\left( { - 3} \right).1 = 37 > 0\) nên phương trình có hai nghiệm. Theo định lí Viète ta có tổng hai nghiệm của phương trình là: \(\frac{{ - 5}}{{ - 3}} = \frac{5}{3}\)
Chọn B
Trả lời câu hỏi Câu 8 trang 19 SBT Toán 9 Kết nối tri thức
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \( - {x^2} - 4x + 6 = 0\). Không giải phương trình, tính giá trị của biểu thức \(M = \frac{1}{{{x_1} + 2}} + \frac{1}{{{x_2} + 2}}\).
A. \(M = 0\).
B. \(M = 1\).
C. \(M = 4\).
D. \(M = - 2\).
Phương pháp giải:
+ Viết định lí Viète để tính tổng và tích các nghiệm \({x_1} + {x_2};{x_1}.{x_2}\).
+ Biến đổi \(M = \frac{{{x_2} + 2 + {x_1} + 2}}{{\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right)}} = \frac{{\left( {{x_1} + {x_2}} \right) + 4}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\), với \({x_1} + {x_2};{x_1}.{x_2}\) đã tính ở trên, ta tính M.
Lời giải chi tiết:
Ta có: \(M = \frac{{{x_2} + 2 + {x_1} + 2}}{{\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right)}} = \frac{{\left( {{x_1} + {x_2}} \right) + 4}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\)
Theo định lí Viète ta có: \({x_1} + {x_2} = \frac{{ - \left( { - 4} \right)}}{{ - 1}} = - 4;{x_1}.{x_2} = \frac{6}{{ - 1}} = - 6\). Do đó, \(M = \frac{{ - 4 + 4}}{{ - 6 + 2.\left( { - 4} \right) + 4}} = 0\).
Chọn A
Trả lời câu hỏi Câu 9 trang 19 SBT Toán 9 Kết nối tri thức
Tìm điều kiện của tham số m để phương trình \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 3m + 5 = 0\) có hai nghiệm phân biệt.
A. \(m \le - 1\).
B. \(m = - 1\).
C. \(m > - 1\).
D. \(m < - 1\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt.
Lời giải chi tiết:
Phương trình đã cho có hai nghiệm phân biệt khi \(\Delta ' > 0\) nên \({\left[ { - \left( {m - 2} \right)} \right]^2} - 1.\left( {{m^2} - 3m + 5} \right) > 0\)
\({m^2} - 4m + 4 - {m^2} + 3m - 5 > 0\)
\( - m - 1 > 0\)
\(m < - 1\)
Chọn D
Trả lời câu hỏi Câu 10 trang 19 SBT Toán 9 Kết nối tri thức
Nếu hai số u, v có tổng là 7 và tích là -8 thì chúng là hai nghiệm của phương trình nào?
A. \({x^2} + 7x - 8 = 0\).
B. \({x^2} - 7x - 8 = 0\).
C. \({x^2} + 7x + 8 = 0\).
D. \({x^2} - 7x + 8 = 0\).
Phương pháp giải:
Hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình \({x^2} - Sx + P = 0\) (điều kiện \({S^2} - 4P \ge 0\)).
Lời giải chi tiết:
Nếu hai số u và v có tổng là 7 và tích là -8 thì chúng là hai nghiệm của phương trình \({x^2} - 7x - 8 = 0\)
Chọn B
Chuyên mục này cung cấp lời giải chi tiết và chính xác cho các câu hỏi trắc nghiệm trong sách bài tập Toán 9 - Kết nối tri thức tập 2, trang 18 và 19. Chúng tôi hiểu rằng việc giải bài tập trắc nghiệm đôi khi có thể gặp khó khăn, đặc biệt là khi các em chưa nắm vững kiến thức nền tảng. Do đó, chúng tôi đã trình bày lời giải một cách rõ ràng, dễ hiểu, kèm theo các giải thích chi tiết để giúp các em hiểu sâu sắc hơn về từng khái niệm và phương pháp giải.
Trang 18 và 19 của sách bài tập Toán 9 - Kết nối tri thức tập 2 tập trung vào các chủ đề sau:
Dưới đây là hướng dẫn giải chi tiết cho từng câu hỏi trắc nghiệm trong sách bài tập Toán 9 - Kết nối tri thức tập 2, trang 18 và 19:
Đề bài: Giải hệ phương trình sau: 2x + y = 5 x - y = 1
Lời giải:
Đề bài: Một người đi xe máy từ A đến B với vận tốc 40km/h. Sau khi đi được 1 giờ, người đó tăng vận tốc lên 50km/h và đến B muộn hơn 30 phút so với dự kiến. Tính quãng đường AB.
Lời giải:
(Giải thích chi tiết các bước giải bài toán, bao gồm việc đặt ẩn, lập phương trình và giải phương trình)
Để giải bài tập trắc nghiệm Toán 9 một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Giaitoan.edu.vn là một nền tảng học toán online uy tín và chất lượng, cung cấp cho các em:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để bắt đầu hành trình chinh phục môn Toán 9!
| Chủ đề | Nội dung chính |
|---|---|
| Hệ phương trình bậc nhất hai ẩn | Phương pháp giải, ứng dụng vào giải bài toán thực tế |
| Hàm số bậc nhất | Định nghĩa, tính chất, đồ thị |
| Phương trình bậc hai một ẩn | Phương pháp giải, ứng dụng |
Chúng tôi hy vọng rằng chuyên mục giải câu hỏi trắc nghiệm trang 18, 19 sách bài tập Toán 9 - Kết nối tri thức tập 2 sẽ giúp các em học tập tốt hơn và đạt kết quả cao trong môn Toán.